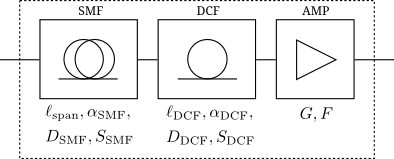This Webdemo shows how signal power, optical signal-to-noise ratio (OSNR) and accumulated dispersion evolve along an optical fiber communication link. The total transmission distance $\ell_\mathrm{tot}$ is divided into $N$ spans of identical length $\ell_\mathrm{span}=\ell_\mathrm{tot}/N$. Each span consists of a single-mode fiber (SMF), a dispersion compensating fiber (DCF) and an optical amplifier (AMP) as shown in the figure. The length $\ell_\mathrm{DCF}$ of the DCF is chosen automatically so that it compensates for the dispersion caused by the SMF. Similarly, the gain $G$ of the AMP makes up for the loss in optical power caused by SMF and DCF.

The dispersion coefficient $D_\mathrm{SMF}$ and the dispersion slope $S_\mathrm{SMF}$ of the SMF are fixed with $D_\mathrm{SMF}=17\,\mathrm{ps/(nm\cdot km)}$ and $S_\mathrm{SMF}=0.053\,\mathrm{ps/(nm^2\cdot km)}$. The dispersion coefficent and slope of the DCF can be chosen freely but its length is calculated automatically, with $\ell_\mathrm{DCF}=-\ell_\mathrm{SMF}D_\mathrm{SMF}/D_\mathrm{DCF}$. All dispersion coefficients and slopes are valid at a wavelength of 1550 nm. For the power plot only one wavelength is considered (single-channel). The OSNR refers to a bandwidth of 12.5 GHz.

For the dispersion plot a wavelength division multiplex (WDM) system with 80 channels and center wavelength 1550 nm is assumed. The plot shows the accumulated dispersion of the channels with lowest, highest and center wavelength, respectively.