Moving persons, cars or other objects cause the environmental channel properties to change. Furthermore signals being reflected by them experience a doppler shift which results in a dispersion in the frequency domain. The shifted rays are superimposed at the receiver which leads to doppler fading introducing time selectivity to the channel. The doppler frequency $f_\mathrm{d}$ is described by:

$$f_\mathrm{d} = \frac{v\cos{\phi}}{\lambda}$$ where

• $v$ denotes the relative velocity
• $\phi$ denotes the phase of a reflected signal
• $\lambda$ is the wavelength of the signal

Due the possibility of being negative as well as positive the bandwith $B$ of a transmitted signal increases to $B + B_{\mathrm{d}}$. Where $B_{\mathrm{d}}$ denotes the doppler spread which is defined by: $$B_{\mathrm{d}} = 2f_{\mathrm{dmax}}$$ The broadening of the spectrum can be seen in the resulting doppler-power-spectrum which models the power-spectral-density as a function of its doppler frequency. From another perspective the doppler-power-spectrum can be descbribed as a probability density function for the random doppler frequency and is therefore a suitable instrument to simulate a doppler fading process. This is being achieved by generating a rayleigh fading signal and filtering it with a doppler filter to approximate the desired doppler-power-spectrum [2].

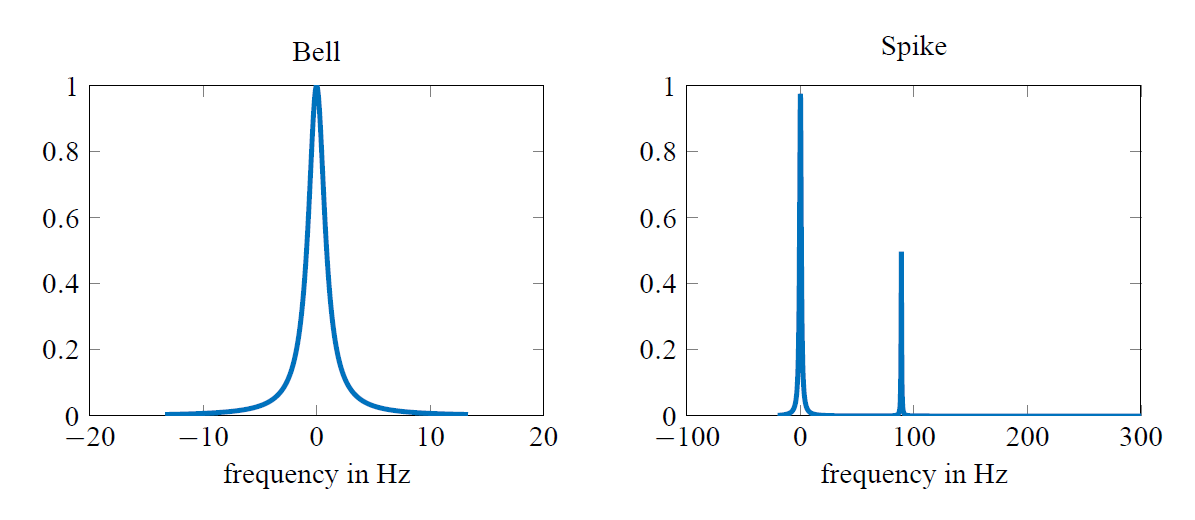
The 802.11n doppler model [3] includes 2 different doppler-power-spectra. The first one is the so called "bell" shaped spectrum simulating slowly moving persons inside a building and is described by

$$S(f)=\frac{1}{1+9\left(\frac{f}{f_{\mathrm{d}}}\right)^2}$$ where $f_{\mathrm{d}}$ denotes the doppler frequency which is defined by $$f_{\mathrm{d}} = \frac{v_0}{\lambda}= \frac{v_0 f_{\mathrm{c}}}{c}$$ where

• $\lambda$ denotes the signal wavelength
• $f_{\mathrm{c}}$ denotes the carrier frequency
• $c$ the speed of light
• $v_0$ is 1.2 km/h and was chosen after a series of measurements

The second one is the "spike" shaped spectrum which was chosen to simulate a car driving with $v_1= 40$ km/h and is used only for the large open space scenario. It is defined by $$S(f)=\frac{1}{1+9\left(\frac{f}{f_{\mathrm{d}}}\right)^2}+\frac{0.5}{1+90000\left(\frac{f-f_{\mathrm{spike}}}{f_{\mathrm{spike}}}\right)^2}$$ where $f_{\mathrm{spike}}$ is calculated the same way as $f_{\mathrm{d}}$ but with $v_1$ as a parameter.