The channel frequency response (spectrum) is not constant over the bandwidth of the transmitted signal and therefore some parts of the signal are attenuated and some are amplified. This effect is due to the multipath propagation of the channel. If echoes arrive at delays similar or greater than the symbol duration these symbols interfere with each other. Because of this interference, a multi-tap time domian equalizer is used to flatten out the spectrum for Single Carrier Modulation.

For comparison purposes, Minimum Mean Squared Error (MMSE) equalization was chosen for single-carrier modulation. Moreover Viterbi equalization is extermly slow for a high order of channel and would not lead to a fair comparison.

MMSE equalization is in comparison to the ZF LS equalization better, because it includes the SNR in the calculation of the filter coefficients. Therefore the goal is to minimize the mean of the Euclidean distance between sent and received symbol with noise. Therefore the filter coefficients are calculated as \begin{equation} \textbf{f}_{\text{MMSE}} = \left(\textbf{H}^H\textbf{H}+\frac{1}{SNR}\textbf{i}\right)^{-1} \textbf{H}^H \textbf{i}. \label{eq:MMSE} \end{equation} Hereby to note is that the filter coefficients need to be normalized first.

OFDM is a common Multi-Carrier modulation scheme. OFDM is most often implemented in the discrete-time domain and therefore the complexity is reduced by using the Fast Fourier Transform (FFT). The number of subcarriers is called $N_{sub}$. For a discrete signal an OFDM symbol in the baseband is given as \begin{equation} x_m = \frac{1}{\sqrt{N_{sub}}}\sum_{n=0}^{N_{sub}-1}s_{0,n}e^{j2\pi \frac{nm}{N_{sub}}} \qquad m=0,..,N_{sub}-1 \label{eq:FFT} \end{equation} Hereby is $s_{0,n}$ a QAM symbol and m is the discrete-time index with respect to the output of FFT, thus defines the baseband bandwidth $B=1/T_m=N_{sub}/T_s$, with $t=m T_m$. $k$ is the discrete-time index at OFDM symbol level, with $t=k T_s$ and $T_s=N_{sub} T_m$. $n$ is the discrete frequency index.

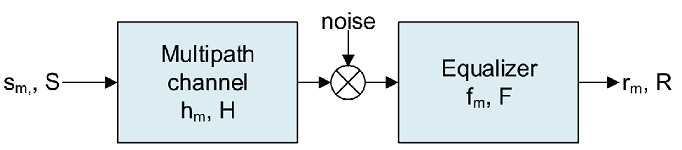
The blockdiagramm of the transmission link is given as

With Floating point operations (Flops) we can measure the complexity of an alogirthm. It measures the number of additions and multiplications executed. The main difference between Single Carrier- and Multi-Carrier Modulation is that Single Carrier modulation uses the convolution and not the FFT for equaliztaion. The number of Flops for FFT and iFFT are the same and are calculated as \begin{equation} \text{Flops}_{\text{FFT}} = N \log_2{N}. \label{eq:Flops_FFT} \end{equation} The number of Flops for the discrete-time convolution calculates as \begin{equation} \text{Flops}_{\text{Conv}} = N ^2. \label{eq:conv} \end{equation}