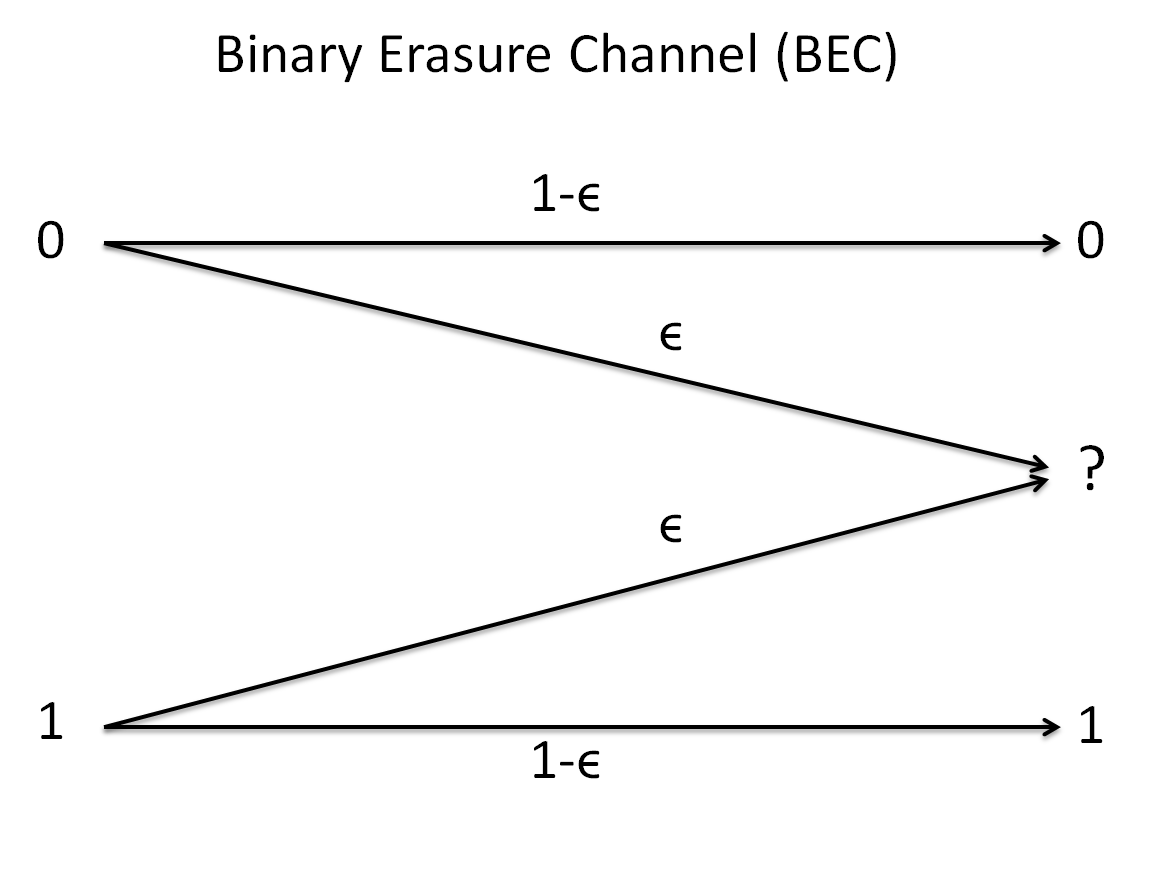
The Binary Erasure Channel (BEC) is one of the simplest channel models to analyze performance. Many applications can be modeled as a Binary Erasure Channel (BEC) such as packet transmission losses. In Binary Erasure Channel (BEC) a bit is transmitted as a 0 or 1 and the receiver either receives correct bit with probability $1-\epsilon$ or an erausure with probability $\epsilon$ as shown above.

The EXIT Chart analysis is divided into two parts as stated previously:

•Variable nodes decoder EXIT curve is given as an exact expression: $$I_{E}^{[V]}=1-\epsilon \, \left(1-I_{A}^{[V]} \right)^{v-1} \:(Regular)$$ $$I_{E}^{[V]}=1-\epsilon \,\sum\limits_{i=1}^{v_{max}} \lambda_i \cdot \left(1-I_{A}^{[V]} \right)^{i-1} \:(Irregular)$$ where $v$ in case of regular is the variable nodes degree (number of 1's in each column of H) and $i$ in case of irregular is a variable nodes degree counter, as for $\lambda_i$ it is the fraction of edges connected to variable nodes of degree $i$. We can clearly observe that the curve depends on $\epsilon$ and any decrease in $\epsilon$ (better channel) will yield a higher curve and better iterative decoding performance.

•Check nodes decoder EXIT curve is given as an exact expression: $$I_{E}^{[C]}= \left(I_{A}^{[C]} \right)^{c-1} \:(Regular)$$ $$I_{E}^{[C]}=\sum\limits_{j=1}^{c_{max}} \rho_j \cdot \left(I_{A}^{[C]} \right)^{j-1} \:(Irregular)$$ where $c$ in case of regular is the check nodes degree (number of 1's in each row of H) and $j$ in case of irregular is a check nodes degree counter, as for $\rho_j$ it is the fraction of edges connected to check nodes of degree $j$. We can clearly observe that the curve is independent from $\epsilon$ (not affected by channel behavior).
The check nodes EXIT curve is plotted with swapped axis ($I_{E}^{[C]}$,$I_{A}^{[C]}$).