In this webdemo we present the following performance measures:

• Symbol Error Rate (SER)
• Bit Error Rate (BER)
• Mutual Information

For the theory we refer to the lecture Communications 3.

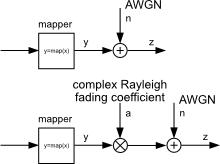
We consider a transmitter with a mapper (QAM, PSK or PAM) and an AWGN channel or Rayleigh fading channel. For the noise we assume a complex Gaussian baseband process, and thus for the noise power spectral density it holds $N_0 = 2 \sigma_n^2$, with $\sigma_n^2$ being the noise power spectral density per real component.

Further, we consider, that the complex Rayleigh fading coefficient $a$ is perfectly known at the receiver. $a$ is iid. complex Gaussian distributed, that is, $a = n_{re} + j n_{im}$, with $n_{re}$ and $n_{im}$ each Gaussian distributed with variance $\sigma^2=\frac{1}{2}$ and mean zero.

The constellations of the mapper are depicted on slide 6.

All performance curves are computed on the fly using Monte-Carlo Simulation.