Transmission Line

Loop resistance $R'$ in $\left[\mathrm{\Omega/m}\right]$,
insulator conductance $G'$ in $\left[\mathrm{S/m}\right]$,
insulator capacitance $C'$ in $\left[\mathrm{F/m}\right]$ and
loop inductance $L'$ in $\left[\mathrm{H/m}\right]$ of transmission line and the angular frequency $\omega=2\pi f$.
Characteristic impedance of transmission line is $Z_{L}\left(\omega\right)=\sqrt{\frac{R'+j\omega L'}{G'+j\omega C'}}$.
Reflection factor at the start of line $r_1=\frac{Z_{1}-Z_{L}}{Z_{1}+Z_{L}}$
Reflection factor at the end of line $r_2=\frac{Z_{2}-Z_{L}}{Z_{2}+Z_{L}}$

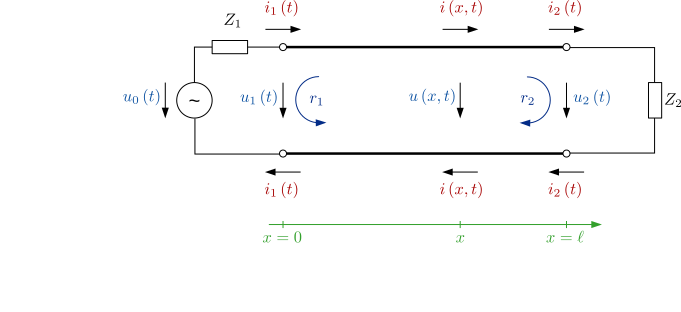
Propagation constant $\gamma\left(\omega\right)=\sqrt{\left(R'+j\omega L'\right)\left(G'+j\omega C'\right)}=\alpha\left(\omega\right) + j\beta\left(\omega\right)$
with the attenuation $e^{-\alpha\left(\omega\right)}$ and wavenumber $\beta\left(\omega\right)=\frac{2\pi}{\lambda}=\frac{\omega}{v_{\mathrm{ph}}}$ with the phase velocity $v_\mathrm{ph}$.

Transfer function is $ F\left(x,\omega\right)=\frac{U\left(x,\omega\right)}{U_{0}\left(\omega\right)}=\frac{Z_{L}}{Z_{1}+Z_{L}}\cdot\frac{1}{1-r_{1}r_{2}\cdot e^{-2\gamma\left(\omega\right)\cdot\ell}}\cdot\left(e^{-\gamma\left(\omega\right)\cdot x}+r_{2}\cdot e^{-\gamma\left(\omega\right)\cdot\left(2\ell-x\right)}\right)$