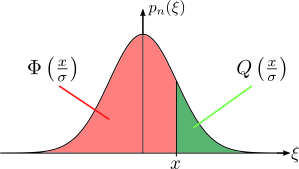
The cumulative distribution function (CDF) of a random variable $X$ is given by the probability of the variable being less or equal to the threshold $x$: $$P[X\le x] = \int_{-\infty}^{x}{ p(\xi) d\xi } = CDF(x)$$ Likewise, the probability of the variable $X$ being greater than the threshold $x$ is given by the complementary CDF (CCDF): $$P[X > x] = \int_{x}^{\infty}{ p(\xi) d\xi } = CCDF(x) = 1-CDF(x)$$ For a standard normal distribution (i.e. $\sigma=1$) the CDF and CCDF are called the $\Phi$-function and $Q$-function, respectively. By the normalization $x'=\frac{x}{\sigma}$, we find the CDF and CCDF for any normal distribution with standard deviation $\sigma$ by $$CDF(x) = P[X\le x] = \Phi\left( \frac{x}{\sigma} \right)$$ and $$CCDF(x) = P[X > x] = Q\left( \frac{x}{\sigma} \right).$$ Furthermore, we have $$P[x_1 < X \le x_2] = Q\left( \frac{x_1}{\sigma} \right) - Q\left( \frac{x_2}{\sigma} \right).$$ Using symmetry, we have the following properties of $\Phi$ and $Q$: $$Q(x') = \Phi(-x') = 1- \Phi(x')$$ $$Q(-x') = 1-Q(x')$$ There are no closed form expressions for $\Phi$ and $Q$. Many numerical software libraries however provide implementations (using series expansion with high accuracy) of the complement error function (erfc), which is directly related to $Q$ via $$Q(x') = \frac{1}{\sqrt{2\pi}} \int_{x'}^{\infty}{ e^{-\frac{1}{2} \xi^2} } = \frac{1}{2} \mathrm{erfc}\left( \frac{x'}{\sqrt{2}} \right)$$