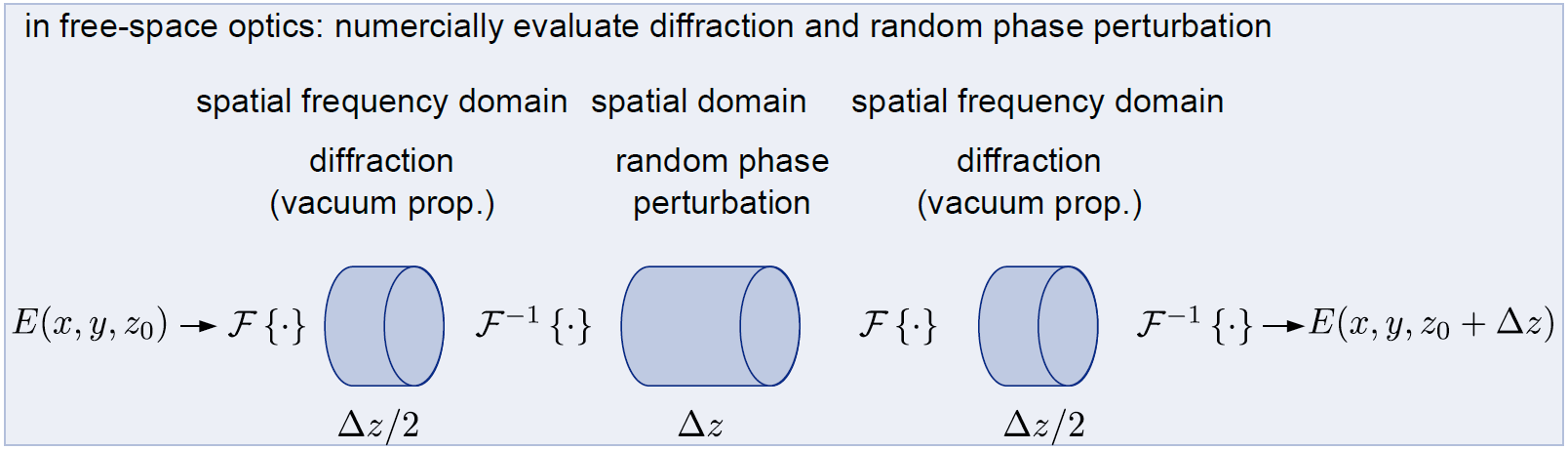
This split step Fourier method is used to numerically compute the propagation of a light beam in turbulent atmosphere. The idea is to split the computation into a free space propagation part accounting for diffaction and a refraction part that accounts for fluctuations of the refractive index. The diffraction is computed in the frequency domain while the refractive index fluctuations are modeled by a random phase screen in spatial domain. The propagation distance in the atmosphere, where the wave is propagating, is partitioned into small steps of size $\Delta z$ and the approach is repeated iteratively along the propagation path.
Let $E(x,y,z)$ represent the envelope of a free space optical signal. The split step Fourier transform iteration for $\Delta z$ then writes as [3]:


$$ E(x,y,z_0+\scriptsize\Delta\normalsize z) = \mathcal{F}^{-1} \Bigg\{ \mathcal{F} \bigg\{ \mathcal{F}^{-1} \Big\{ \mathcal{F}\big\{E(x,y,z_0)\big\} e^{i\frac{\left(\kappa^{2}_{x}+\kappa^{2}_{y}\right)\frac{\Delta z}{2}}{2k_{0}}} \Big\} e^{-iS \Delta z} \bigg\} e^{i\frac{\left(\kappa^{2}_{x}+\kappa^{2}_{y}\right)\frac{\Delta z}{2}}{2k_{0}}} \Bigg\} $$
$\kappa_{x}$ and $\kappa_{y}$ are the corresponding spatial angular frequency components in the $x$ and $y$ direction with $\kappa = \sqrt{\left(\kappa^2_x+\kappa^2_y\right)}$

$k_{0}$ = $\frac{2\pi}{\lambda}$ is the free space wavenumber

$i\frac{\left(\kappa^2_x+\kappa^2_y\right)\frac{\Delta z}{2}}{2k_0}$ and $-iS \Delta z$ represents respectively the diffraction $\mathcal{D}$ and refraction $\mathcal{R}$ operator [2]