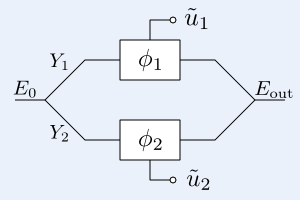
The Mach-Zehnder modulator (MZM) consists of two phase modulators that allow changing the refractive index of a waveguide proportionally to a driving voltage $\tilde u_i = u_i + U_\mathrm{i,DC}$, $i \in \{1,2\}$. The figure shows a so-called differential (or "dual-drive") MZM that enables driving the two phase modulators independently, though here we restrict to $\tilde u_1 = s \tilde u_2$, $s \in \{-1, 1\}$. At the MZM input the incoming continous light wave is split with the factors $Y_1$ and $Y_2$ and phase shifted by $\phi_1$ and $\phi_2$, respectively. At its output the phase shifted light waves interfere producing the output electrical field $\tilde E_\mathrm{out}$. The complex envelope of this field is given by $$ E_\mathrm{out} = \frac{E_0}{\sqrt{2}} \left[ Y_1 \mathrm e^{\mathrm j \left( \frac{u_1 + U_\mathrm{1,DC}}{U_\pi} \right) \pi} + Y_2 \mathrm e^{\mathrm j s\left( \frac{u_1 + U_\mathrm{1,DC}}{U_\pi} \right) \pi}\right] $$ There are two important cases ($Y_1 = Y_2 = \sqrt{0.5}$):

Mode of operation	push-push ($s=1$)	push-pull ($s=-1$)
Application	Phase modulation	Amplitude modulation
Transfer function	$E_\mathrm{out}=E_0 \mathrm e^{\mathrm j\left( \frac{u_1 + U_\mathrm{1,DC}}{U_\pi} \right)\pi}$	$E_\mathrm{out}=E_0 \cos \left( \frac{u_1 + U_\mathrm{1,DC}}{U_\pi} \pi \right)$

Generally, $Y_1 = \sqrt{0.5 + \epsilon}$ and $Y_2 = \sqrt{0.5 - \epsilon}$. Imperfect splitting ($\epsilon \neq 0$) leads to a finite extinction ratio, i. e. the light at the MZM output cannot be extinguished completely. The extinction ratio is therefore defined as the ratio of the maximum output power to the minimum output power and given by $\rho = (Y_1 + Y_2)^2/(Y_1 - Y_2)^2$. On the following slide the field, power and phase transfer functions can be studied for different operational modes, bias voltages and extinction ratios.