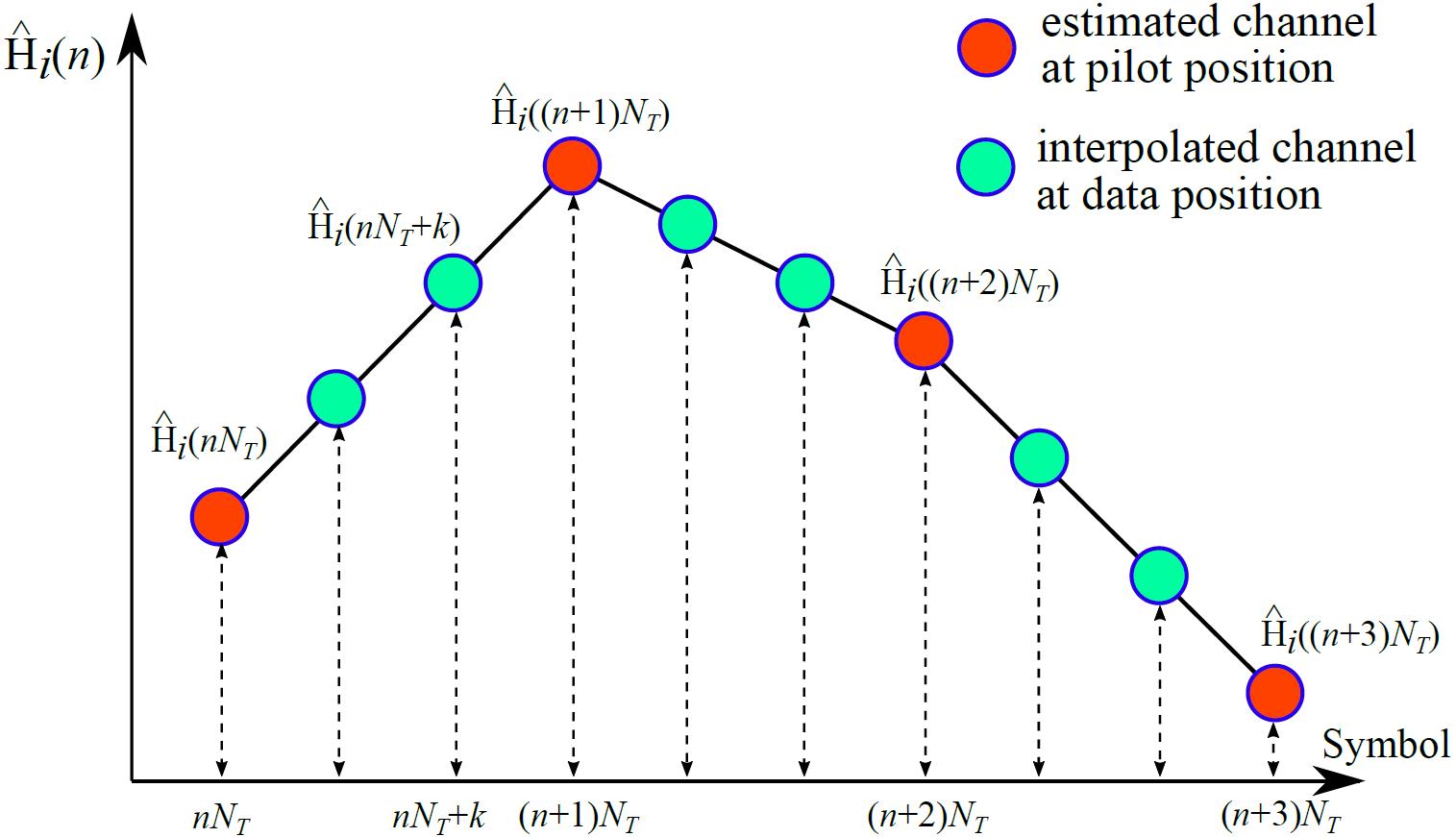
Linear interpolation is the simplest method of curve fitting using linear polynomials to estimate the channel at non-pilot positions within the range of a discrete set of known pilots. The linear interpolation is the straight line between adjacent pilots (both in the time and the frequency domain), which is given by

$$\hat{\mathrm{H}}_{i}\left(nN_{T}+k\right)=(1-\alpha)\cdot\hat{\mathrm{H}}_{i}\left(nN_{T}\right)+\alpha\cdot\hat{\mathrm{H}}_{i}\left(\left(n+1\right)N_{T}\right), 0\leq n\leq N_{p}-1$$

where
$\alpha$ is the $\frac{k}{N_{T}}$,
$N_T$ is the pilot spacing in the time domain,
$N_P$ is the total number of pilot symbols in the time domain.

The interpolation in the frequency domain is the same as that in the time domain.

The linear interpolation method can be illustrated geometrically in the figure below.