Graphical Representation

To represents LDPC codes, there are different types of graphical tools. Among them the Tanner graph is an effective graphical representation of LDPC codes. It provides the complete representation of the code, and also helps to describe the decoding algorithm.

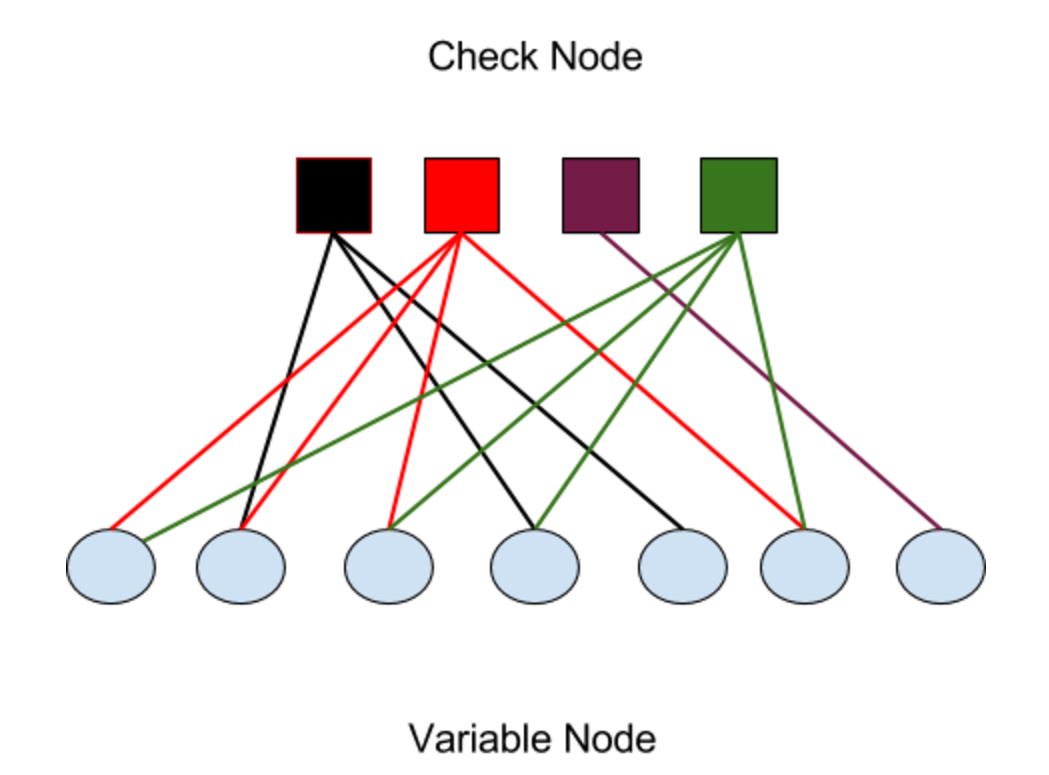
Tanner graphs are basically bipartite graphs, i.e., there are two disjuncts sets of nodes.

The two types of nodes are Variable Nodes (VND) and Check Nodes (CND).

•Variable Nodes: Represent the code bits. Thus, each of the $n$ columns of $\mathbf{H}$ matrix is represented by one VND.

•Check Nodes: Represent the code constraints. Thus, each of $m$ rows of $\mathbf{H}$ matrix is represented by one CND.

Each "Variable node" $v_i$ is going to connect to a "check node" $c_j$, if $\mathbf{H}_{i,j}=1$ as shown below: $$H=\begin{pmatrix} 0& 1 & 0 & 1 & 1 & 0 & 0\\ 1& 1 & 1 & 0 & 0 & 1 & 0\\ 0& 0 & 0 & 0 & 0 & 0 & 1\\ 1& 0 & 1 & 1 & 0 & 1 & 0 \end{pmatrix}$$

Conversion of the protograph matrix $\mathbf{B}$ to Parity check matrix $\mathbf{H}$

In most of the standards, a base matrix $\mathbf{B}$ is given in order to define the LDPC code. However, $\mathbf{B}$ needs to be converted into a $\mathbf{H}$ matrix using a lifting factor $L$. Lifting means that each (integer) entry of $\mathbf{B}$ is replaced by a permuted $L \times L$ identity-matrix, for example in Docsis 3.1 short code there is a $54\times54$ subblock matrix for each block. We take the identical matrix $\mathbf{I}$ and then circular shift this matrix according to the base matrix entry $\mathbf{B}_{i,j}$, then we get the desired $\mathbf{H}$ matrix.
For example, suppose a protograph matrix $\mathbf{B}=2\times 2$ and $L=3$. Now converting from $\mathbf{B}$ to $\mathbf{H}$ can be done as shown below. \[ B = \begin{pmatrix} 2 & 3 \\ 0 & 1 \end{pmatrix} \text{ , } I = \begin{pmatrix} 1 & 0 & 0 \\ 0& 1 & 0 \\0 & 0 & 1 \end{pmatrix} \] \[ H= \left[ \begin{array}{cc} \left[\begin{array}{ccc} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array}\right] & \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] \\ \left[\begin{array}{ccc} 1 & 0& 0 \\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right] & \left[\begin{array}{ccc} 0 & 1 & 0\\ 0 & 0 & 1\\ 1 & 0 & 0 \end{array}\right] \\ \end{array}\right] \] \[ H = \begin{bmatrix} 0 & 0 & 1 & 1 & 0 & 0\\ 1 & 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 & 1\\ 1 & 0 & 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 1 & 0 & 0 \end{bmatrix} \]

For a more detailed explanation of the decoder go to demo Peeling Decoder for Graph Based Codes.