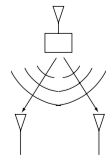
Multiuser Capacity | Webdemo | Institute of Telecommunications, University of Stuttgart

Downlink: NOMA vs OMA

The downlink communication features a single transmitter (the base-station) sending separate information to multiple users. The baseband downlink AWGN channel with two users is $$ y_k[m]=h_k \cdot x[m]+ w_k[m] $$ where $w_k[m] \sim \mathcal{C N}\left(0,N_0\right)$ is i.i.d. complex Gaussian noise. and $y_k\left[m\right]$ is the received signal at user $k$ at time $m$, for both the users $k$ = 1􏷩, 2. Here $h_k$ is the fixed channel gain corresponding to user $k$ and indicates the condition of the channel. The transmit signal $x[m]$ has an average power constraint of $P$, which will be allocated to each user in the system.

Under asymmetric condition, when $\left|h_1\right|$ < $\left|h_2\right|$, NOMA follows this scheme: user 1 treats the signal of user 2 as noise and decodes its data from $y_1$, user 2 decodes the data of user 1 and substract the signal of user 1 from $y_2$ before decode its own data. The decoding process of user 2 is much like SIC. With the power allocation fraction $\beta$, the following rate pair can be achieved: $$ R_1= \log_{2}\left(1+\frac{P_1\left|h_1\right|^2}{P_2\left|h_1\right|^2+N_0}\right) $$ $$ R_2= \log_{2}\left(1+\frac{P_2\left|h_2\right|^2}{N_0}\right) $$ where $$ P_1=\beta \cdot P $$ $$ P_2=\left(1-\beta\right) \cdot P $$ $$ 0<\beta<1 $$

With orthogonal schemes, as introduced in slide 3, another fraction $\alpha$ is needed to split degree of freedom between users. For each combination of power split $\beta$ and degree-of-freedom split $\alpha$, the following rate pair can be achieved: $$ R_1= \alpha \log_{2}\left(1+\frac{P_1\left|h_1\right|^2}{\alpha N_0}\right) $$ $$ R_2= \left(1-\alpha\right) \log_{2}\left(1+\frac{P_2\left|h_2\right|^2}{\left(1-\alpha\right) N_0}\right) $$ where $$ P_1=\beta \cdot P $$ $$ P_2=\left(1-\beta\right) \cdot P $$ $$ 0<\alpha<1 $$ $$ 0<\beta<1 $$ Here, both fraction $\alpha$ and $\beta$ should be jointly optimized to compute the boundary.

There is one thing that has to be paid attention to: under symmetric condition, namely when $\left|h_1\right|$ = $\left|h_2\right|$, the performance of NOMA and OMA are the same. On the contrast, under asymmetric condition, NOMA outperforms OMA and the gap between them are more obvious when the asymmetry deepens.