Radar

Radar, an acronym for Radio Detection and Ranging, is a common remote sensing technology. Radar is often utilized to determine the distance, angle, and velocity of objects. Unlike many optical systems, Radar can be used during day and night and is not weather dependent.
The core principle of radar is to send electromagnetic waves and to analyze the received reflections to gain information about the environment.

Historically, radar has been used for military or large-scale civilian applications. This includes aviation, transport, navigation, and collision avoidance. The "first electromagnetic echo-location device" was developed in 1904 by Christian Hülsmeyer as a ship anticollision system [1].
Since then, radar has experienced considerable development. During WW2 and the Korean War, the need for enemy aircraft detection led to the development of the Doppler Radar. A frequency change introduced by the Doppler effect allowed to determine the relative velocity of an aircraft [2]. With the advent of mass manufactured small and cheap electronics, new applications have evolved. A prominent example would be automotive radar, which is a core technology for driver assistance and autonomous driving.

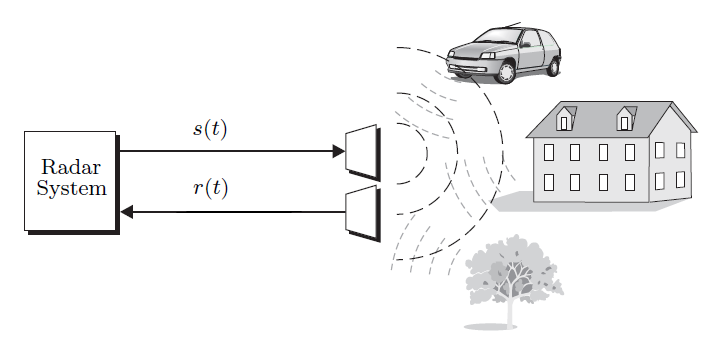
A radar system utilizes antennas to transmit signals $s(t)$ and receive the backscattered echoes $r(t)$ of the original signals. The backscattered signal is a superposition of reflections of the original signal caused by surrounding objects. By analyzing the backscattered signal, the locations and velocities of the objects can be determined [3].

OFDM

OFDM (orthogonal frequency-division multiplexing) is a commonly used digital transmission scheme. It is utilized in wireless networks (IEEE 802.11), digital television, 4G/5G mobile communications and many more. OFDM is (de-)modulated by computationally efficient FFT techniques.
As the name indicates, OFDM divides the available bandwidth between a number of subcarriers. Like other FDM schemes, OFDM transmits several symbols at a longer symbol time $T$ than single carrier schemes achieving the same data rate. This helps prevent ISI (Inter Symbol Interference) and makes OFDM a good choice for environments with multipath propagation.
In addition, OFDM offers a high spectral efficiency by utilizing orthogonal frequencies. This allows for an overlap in the frequency domain wtihout causing ICI (Inter Carrier Interference) [5]. The orthogonality is achieved by selecting a constant subcarrier spacing $\Delta f=|f_0-f_1|$ of the inverse symbol duration,

\begin{equation} \Delta f = \frac{1}{T}. \end{equation} The subcarrier frequency of a subcarrier $k$ can therefore be determined by \begin{equation} f_k=f_0+k\Delta f, k \in \mathbb{Z}. \end{equation} The orthogonality condition holds, even for spectrally inefficient rectangular pulse shaping [6]. \begin{equation} \frac{1}{T}\int_{0}^T e^{j2\pi f_0t}e^{-j2\pi f_1t} dt = \begin{cases} 0\quad |f_0-f_1|=k\Delta f, k \in \mathbb{Z}\setminus 0\\ 1\quad f_0=f_1 \end{cases} \end{equation}

Why OFDM Radar

Radar and communication systems are both based on transmitting and receiving electromagnetic waves. Due to this similarity between radar and communications a fusion of both systems seems practical. A combined system would require less hardware, bandwidth, and energy than two separate systems. This would result in reduced production and operation costs.