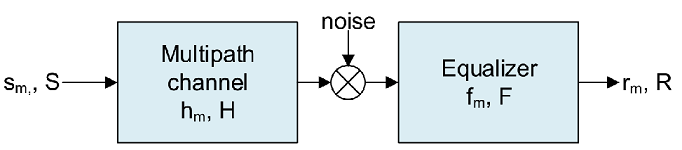
The channel frequency response (spectrum) is not constant over the bandwidth of the transmitted signal and therefore some parts of the signal are attenuated and some are amplified. This effect is due to the multipath propagation of the channel. If echoes arrive at delays similar or greater than the symbol duration these symbols interfere with each other. Because of this interference, a multi-tap time domian equalizer is used to flatten out the spectrum for Single Carrier Modulation.

Zero-Forcing, Least squares is a linear equalizer where the filter coefficients are calculated as \begin{equation} \textbf{f}_{\text{ZF LS}} = \underbrace{\left(\textbf{H}^H \textbf{H}\right)^{-1} \textbf{H}^H}_{\text{pseudo-inverse}} \textbf{i}. \label{eq:filter_coef_ZFLS} \end{equation} Hereby the vector $i$ is the wanted received vector, for example (with D=1) \begin{equation} \textbf{i} = (1 \quad 0 \quad 0 \quad 0)^T \label{eq:wanted_received_vector} \end{equation}

MMSE equalization is in comparison to the ZF LS equalization better, because it includes the SNR in the calculation of the filter coefficients. Therefore the goal is to minimize the mean of the Euclidean distance between sent and received symbol with noise. Therefore the filter coefficients are calculated as \begin{equation} \textbf{f}_{\text{MMSE}} = \left(\textbf{H}^H\textbf{H}+\frac{1}{SNR}\textbf{i}\right)^{-1} \textbf{H}^H \textbf{i}. \label{eq:MMSE} \end{equation} Note is that the filter coefficients need to be normalized first.

Rayleigh fading channel with and without a $d^{-2}$ path loss attenuation profile was used. Therefore the channel coefficients are given as \begin{equation} h_m = \sqrt{\frac{d_l}{\beta}} \cdot \text{RV}_{G} \label{eq:rayleigh_decay_model} \end{equation} with $\text{RV}_{G}$ being a Gaussian random variable that is $\mathcal{N}\left(0,\frac{1}{L+1}\right)$-distributed and where \begin{equation} \beta = \frac{1}{N}\sum_{i=1}^{N}{\text{E}_{\text{channel}}} \label{eq:beta} \end{equation} is a normalization factor to even out the energy loss through the attenuation profile. The attenuation profile (free space path loss) is given as \begin{equation} d_m = \frac{1}{(\alpha m+1)^2} \label{eq:delay_curve} \end{equation} with \begin{equation} \alpha = \frac{1}{L} \left(\frac{1}{\sqrt{\text{E}_\text{tap}}}-1\right). \label{eq:alpha} \end{equation} For testing the implemented script, a given channel \begin{equation} H_1(z) = 1 + z^{-1} - \frac{1}{2}z^{-2} \label{eq:givenchannel} \end{equation} was used. ZF LS equalizer leaves out those channel impulse responses $h_m$ that would have lead to unstable equalizer filters. Therefore not a perfect Rayleigh distribution is shown.