LDPC Codes are popular nowadays as they are capacity approaching (yield results very close to "Shannon Limit") due to the existence of efficient decoding techniques. Maximum A Posteriori (MAP) Decoding can be applied to LDPC Codes. However, the complexity is large and grows exponentially with large codes and so it would be infeasible to implement in most applications. An alternative simple graph-based iterative sub-optimal decoding algorithm which yields very good results. The technique is based on the "Tanner Graph".

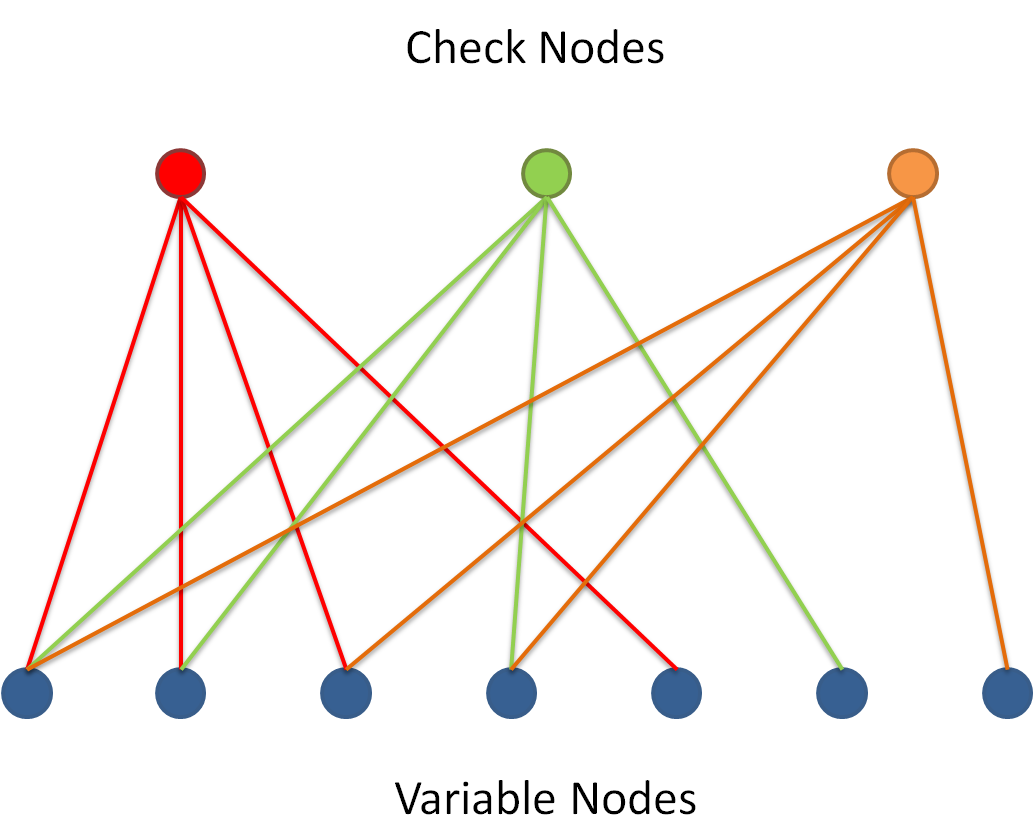
A Tanner Graph is a bipartite graph which means that nodes are divided into two distinctive sets:

•Variable Nodes: of length n each corresponding to a code bit and a column in (H)

•Check Nodes: of length m=n-k each corresponding to a parity check constraint and a row in (H)

Each "Variable node" $x_j$ is connected with an edge to a "Check node" $y_j$, if $H_{i,j}=1$ as shown below: $$H=\begin{pmatrix} 1& 1 & 1 & 0 & 1 & 0 & 0\\ 1& 1 & 0 & 1 & 0 & 1 & 0\\ 1& 0 & 1 & 1 & 0 & 0 & 1 \end{pmatrix}$$

For more detailed explanation of decoder go to demo Peeling Decoder for Graph Based Codes.