The Additive White Gaussian Noise (AWGN) Channel is the most popular channel in the field of communications and it is considered as a good model for many applications as satellite and deep space communications. However, AWGN is a bit more complicated in analysis than BEC and it is a more general channel. The channel is named this way because of its characterstics:

•Additive: Noise is added to symbols.

•White: Uniform power over all frequency bands.

•Gaussian: As it models many random processes and due to the central limit theorem (summation of many random processes result in a normal distribution $N(0,\sigma^2)$ with 0 mean and $\sigma^2$ variance)

The EXIT Chart analysis is divided into two parts as stated previously:

•The variable nodes decoder EXIT curve is given as an approximate expression: $$I_{E}^{[V]} \approx J \left(\sqrt{(v-1)\,J^{-1} \left(I_{A}^{[V]} \right)^{2}+8R\,\dfrac{E_b}{N_o}} \right) \: (Regular)$$ $$I_{E}^{[V]} \approx \sum\limits_{i=1}^{v_{max}} \lambda_i \cdot J \left(\sqrt{(i-1)\,J^{-1} \left(I_{A}^{[V]} \right)^{2}+8R\,\dfrac{E_b}{N_o}} \right) \: (Irregular)$$ where $v$ in case of regular is the variable nodes degree (number of 1's in each column of H) and $i$ in case of irregular is a variable nodes degree counter, as for $\lambda_i$ it is the fraction of edges connected to variable nodes of degree $i$. We can clearly observe that the curve depends on rate and $\dfrac{E_b}{N_o}$ (Signal to Noise Ratio (SNR)) and any increase in SNR (better channel) will yield a higher curve and better iterative decoding performance.

•The check nodes decoder EXIT curve is given as an exact expression: $$I_{E}^{[C]} \approx 1-J \left(\sqrt{c-1}\,J^{-1} \left(1-I_{A}^{[C]} \right) \right) \: (Regular)$$ $$I_{E}^{[C]} \approx 1-\sum\limits_{j=1}^{c_{max}} \rho_j \cdot J \left(\sqrt{j-1}\,J^{-1} \left(1-I_{A}^{[C]} \right) \right) \: (Irregular)$$ where $c$ in case of regular is the check nodes degree (number of 1's in each row of H) and $j$ in case of irregular is a check nodes degree counter, as for $\rho_j$ it is the fraction of edges connected to check nodes of degree $j$. We can clearly observe that the curve is independent from SNR (not affected by channel behavior).
Check nodes EXIT curve is plotted with swapped axis ($I_{E}^{[C]}$,$I_{A}^{[C]}$).

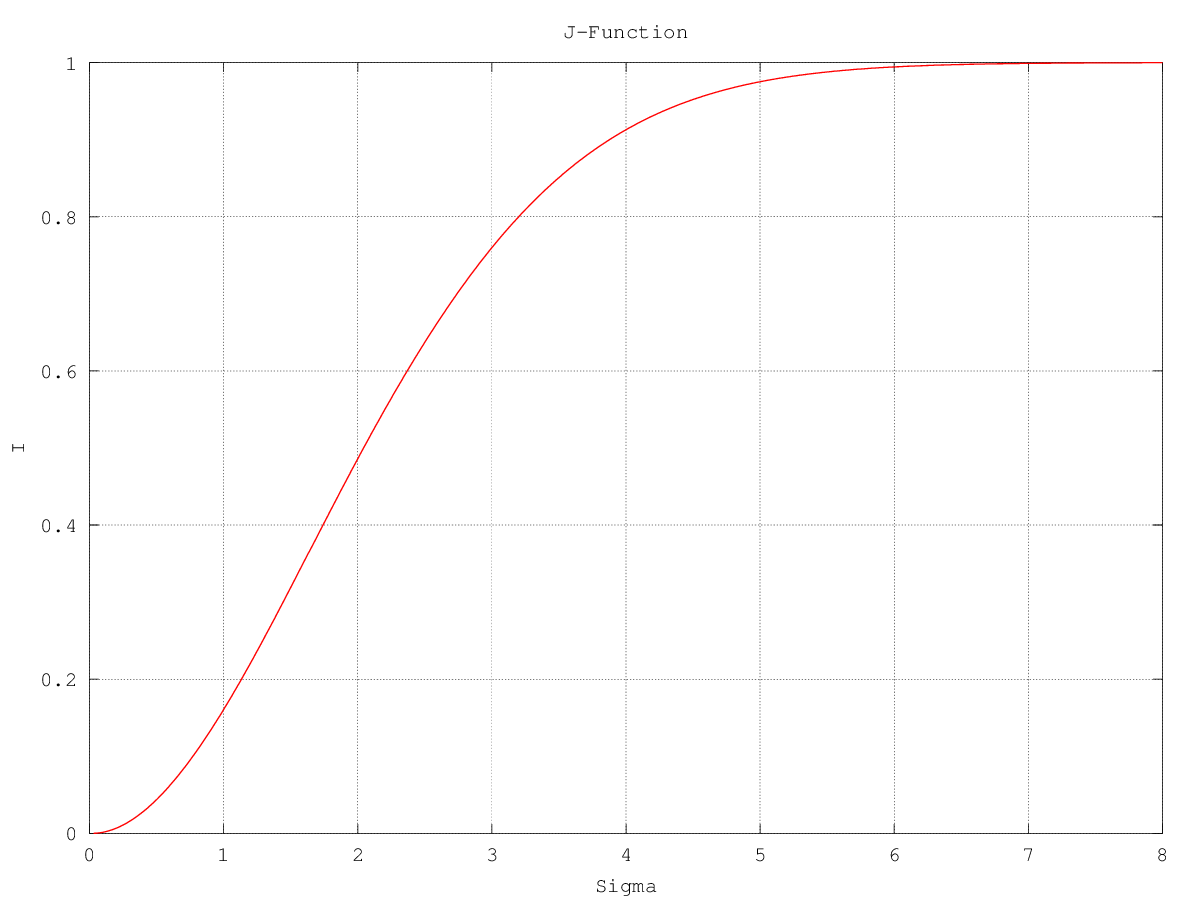
Note: The J-Function is a monotonically increasing function that maps $\sigma$ to mutual information I as shown below, and the inverse J-Function can do the inverse operation.