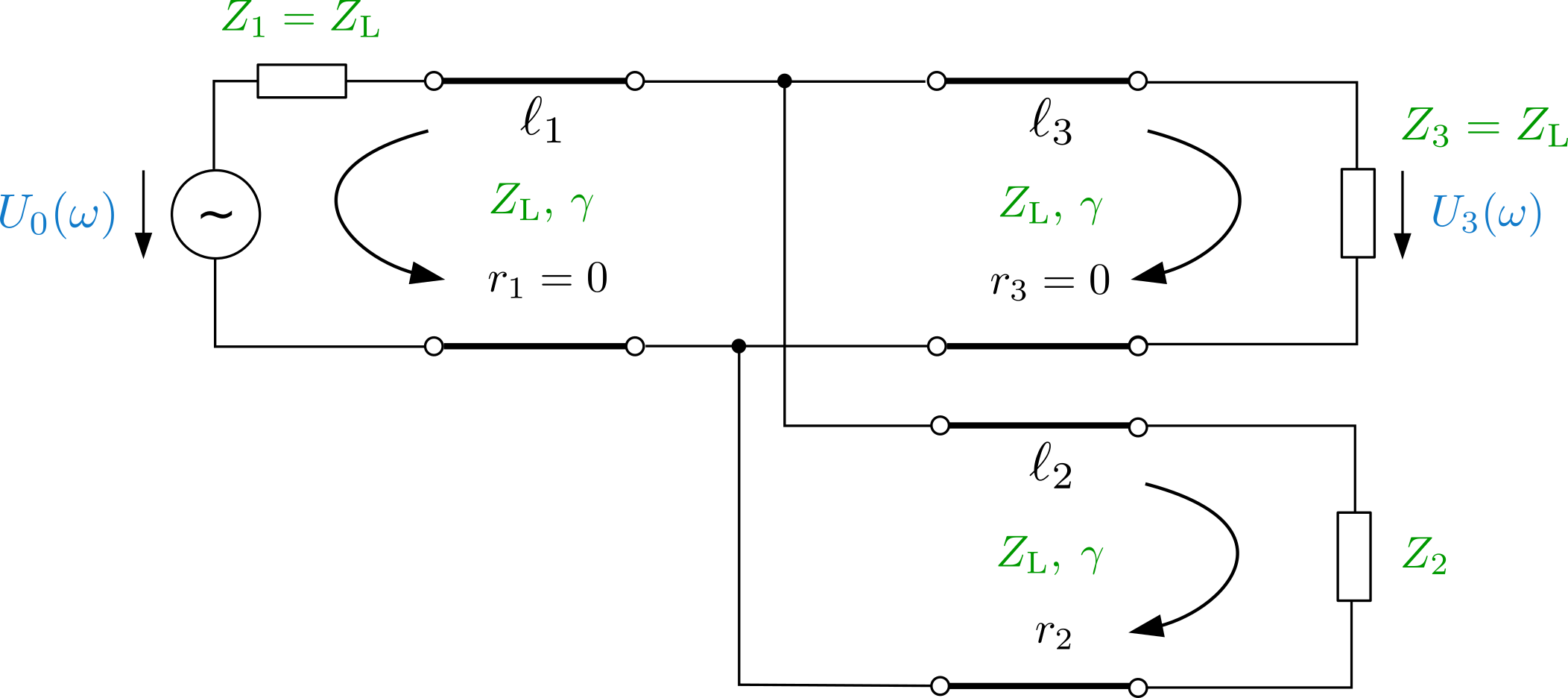
The following webdemo demonstrates the channel characteristics of transmission line topology (shown below). In this case, we introduce three transmission lines with same characteristic impedance $Z_\text{L}$, and corresponding arbitrary length $\ell_1$, $\ell_2$, $\ell_3$. The reflection coefficients $r_i$ are given by $r_i = \frac{Z_i-Z_\text{L}}{Z_i+Z_\text{L}}$ with $Z_1$, $Z_2$ and $Z_3$ being the impedance at the input, at the end of $\ell_2$ or at output of the line, respectively. For simplicity we assume impedance matching at input and output,that is $r_1$ = 0, $r_3$= 0, and a real variable $r_2$ at the end of $\ell_2$. Particularly for this topology ($\ell_2$ and $\ell_3$ are in parallel), we have one more reflection coefficient $r_4 = -\frac{1}{3}$ at the junction of three transmission lines. Additionally, we introduce transmission coefficient $\gamma = \alpha+j\beta$ where $\alpha$ denotes a constant attenuation coefficient, and $\beta$ is phase coefficient which is linear in $\omega$. Attenuation $\alpha$ is given in $\frac{\text{dB}}{\text{m}}$ and can be converted to $\frac{\text{Np}}{\text{m}}$ by $\alpha \big|_\frac{\text{Np}}{\text{m}} = \frac{ln(10)}{20} \cdot \alpha \big|_\frac{\text{dB}}{\text{m}}$. $\beta$ is related to the phase velocity ($v_{\text{ph}}=\frac{\omega}{\beta}$) and $\omega$ ($\omega = {2\pi f}$). Therefore, $\gamma = \alpha+j\beta = \alpha+j \frac{2\pi f}{v_{\text{ph}}}$.

This demo focuses on transfer function of each reflection iteration denoted as $H_k(f)$ as well as overall transfer function $H_{\text{sum}}(f)$ which is the sum up of all iterations ($N_{\text{iter}}$). The general expression for a single transmission line known to be $$ H(x,f) = \frac{1-r_1}{2} \sum_{n=0}^{\infty}(r_1r_2)^ne^{-\alpha(2\ell n+x)}e^{-j \cdot 2 \pi f\frac{2\ell n+x}{v_{\text{ph}}}} + \frac{1-r_1}{2}r_2 \sum_{n=0}^{\infty}(r_1r_2)^ne^{-\alpha(2\ell (n+1)-x)}e^{-j \cdot 2 \pi f\frac{2\ell (n+1)-x}{v_{\text{ph}}}} $$ The equation of individual iterations and overall transfer function ^[1] of the given setup are expressed as

At the end of $\ell_1$: $$ H_0(f) = \frac{1-r_1}{2} e^{-\gamma \ell_1} $$

$1^{\text{st}}$ iteration: $$ H_1(f) = H_0(f) \cdot \frac{2}{3} e^{-\gamma \ell_3} $$

$2^{\text{nd}}$ iteration: $$ H_2(f) = H_0(f) \cdot \frac{2}{3} e^{-\gamma \ell_3} \cdot \frac{2}{3} e^{-\gamma \cdot 2 \ell_2} \cdot r_2 $$

$3^{\text{rd}}$ iteration: $$ H_3(f) = H_0(f) \cdot \frac{2}{3} e^{-\gamma \ell_3} \cdot \frac{2}{3} e^{-\gamma \cdot 2 \ell_2} \cdot (r_2)^2 \cdot \left(-\frac{1}{3}\right) e^{-\gamma \cdot 2 \ell_2} $$

$4^{\text{th}}$ iteration: $$ H_4(f) = H_0(f) \cdot \frac{2}{3} e^{-\gamma \ell_3} \cdot \frac{2}{3} e^{-\gamma \cdot 2 \ell_2} \cdot (r_2)^3 \cdot \left[\left(-\frac{1}{3}\right) e^{-\gamma \cdot 2 \ell_2}\right]^2 $$

$k^{\text{th}}$ ($2 \leq k \leq N_{\text{iter}}$) iteration: $$ H_k(f) = H_0(f) \cdot \frac{2}{3} e^{-\gamma \ell_3} \cdot \frac{2}{3} \cdot (r_2)^{k-1} \cdot \left(-\frac{1}{3}\right)^{k-2} e^{-(k-1) \gamma \cdot 2 \ell_2} $$

Overall transfer function $H_{\text{sum}}(f)$: $$ H_{\text{sum}}(f) = H_1(f) +\sum_{k=2}^{N_{\text{iter}}} H_k(f) $$

In the first demo, $H(f)$ is shown per iteration (frequency flat). The overall transfer function $H_{\text{sum}}(f)$ is shown as the thick blue curve with frequency selectivity (constructive and destructive effect).

The comparison between overall transfer function $H_{\text{sum}}(f)$ and its imaginary part $\operatorname{Im}\{H_{\text{sum}}(f)\}$, as well as its absolute value $\left|H_{\text{sum}}(f)\right|$ are shown in the second and the third demo respectively.