5G LDPC Codes | Webdemo | Institute of Telecommunications, University of Stuttgart

Rate Matching

Message bit puncturing

The first $2Z$ columns of $\mathbf{H}$ are comparably dense, meaning that many parity-check equations depend on the reliability of the first $2Z$ bits of a codeword $\mathbf{c}$. This is why $\left[c_i\right]_{1\leq i \leq 2Z}$ is never transmitted. If the message bit puncturing were not done, an error in $\left[c_i\right]_{1\leq i \leq 2Z}$ would cause severe error propagation. With puncturing of message bits, additional $2Z$ parity bits can be sent without changing $R_{\mathrm{c}}=\frac{K}{N}$. The receiver still uses the respective part of $\mathbf{H}$ for decoding.

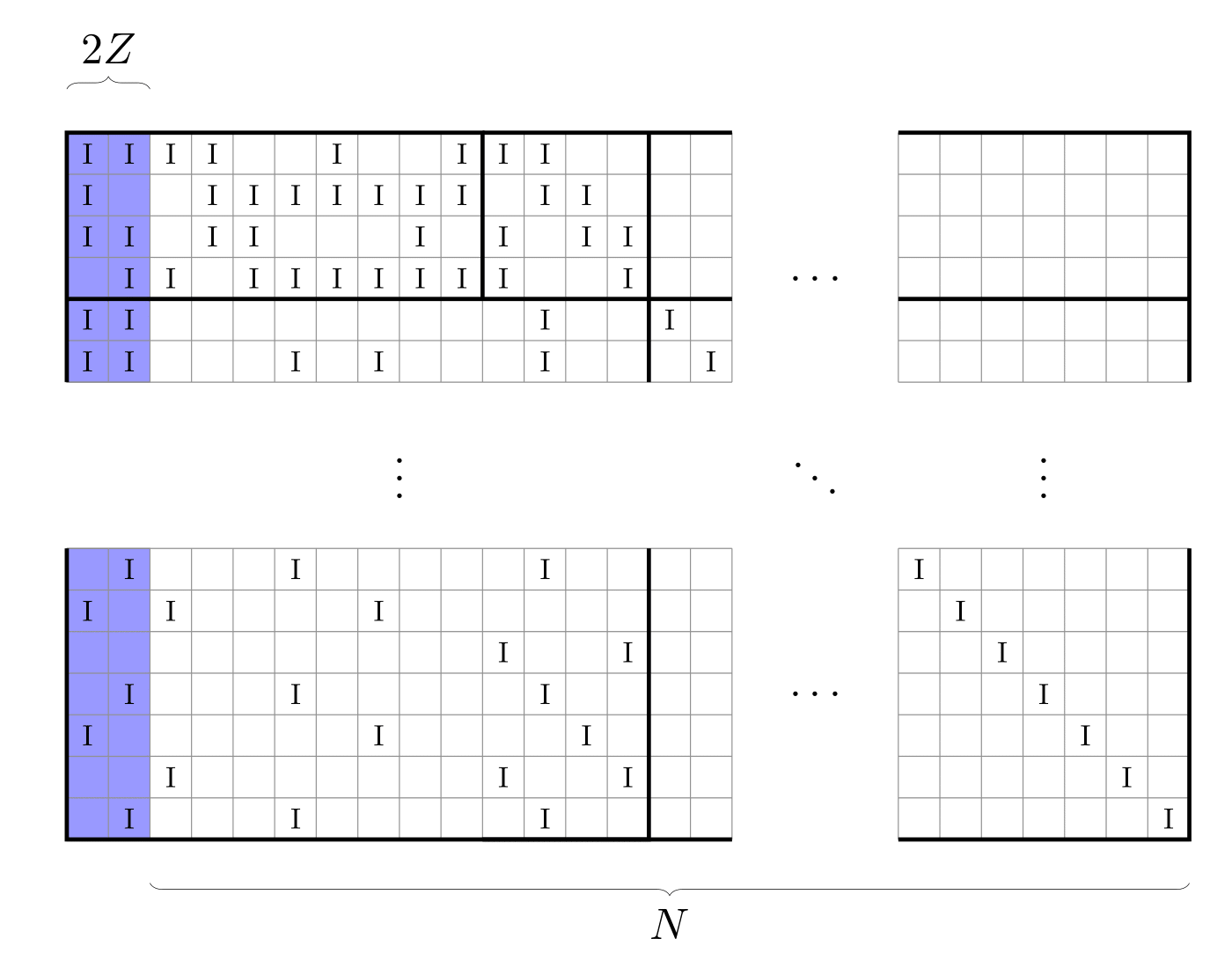
Parity bit puncturing

Not transmitting the $P$ last parity bits of $\mathbf{c}$ reduces $N$ effectively, resulting in an increased $R_{\mathrm{c}}$. For LDPC codes this so called parity bit puncturing can be implemented by disregarding the respective rows and columns of $\mathbf{H}$ as displayed in the figure below.

Only using a submatrix of $\mathbf{H}$ reduces the computational cost for encoding and decoding and can therefore increase the throughput for high $R_{\mathrm{c}}$.

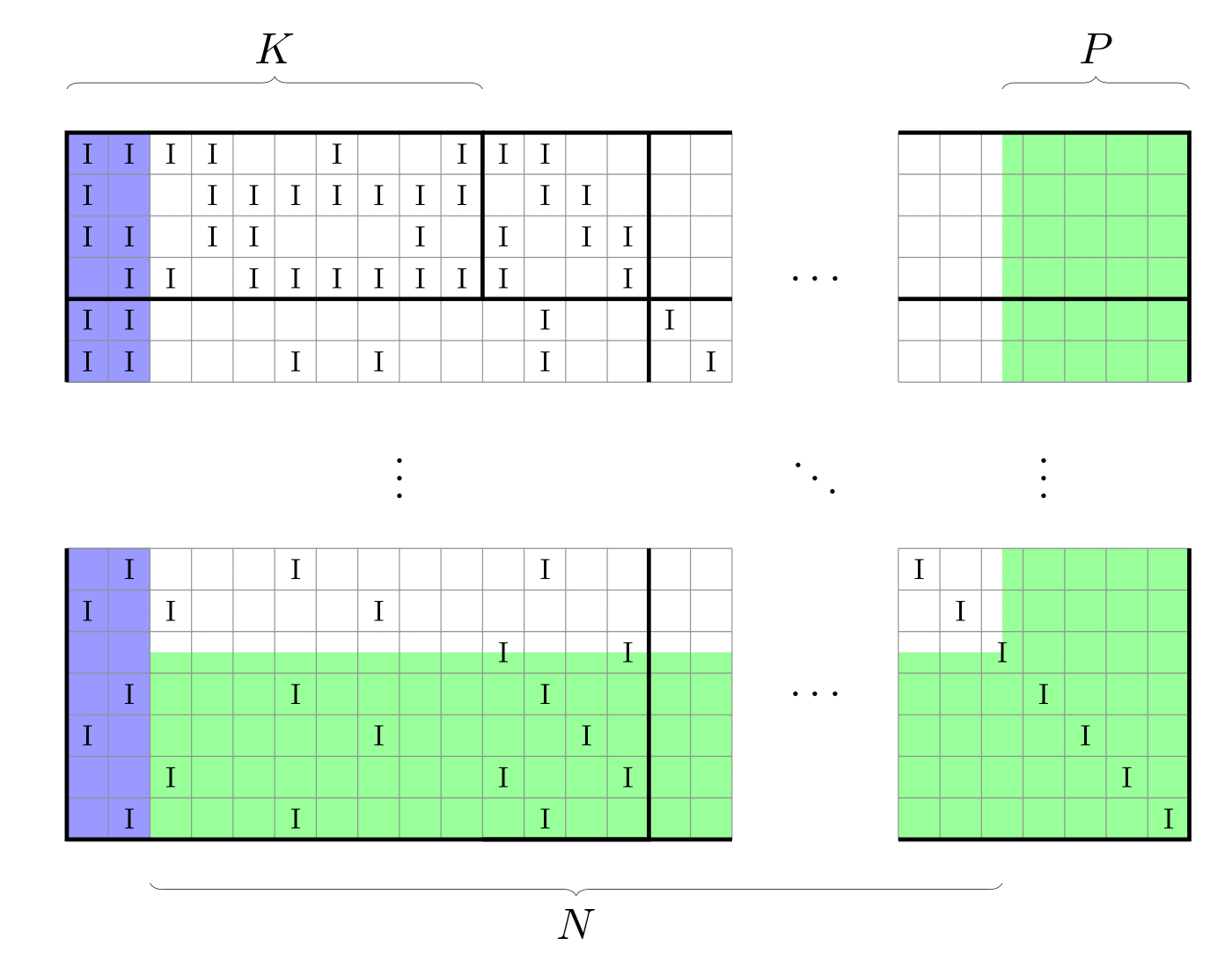
Figure : Parity bit puncturing for 5G LDPC code

Message bit shortening

Message bit shortening typically refers to zero-padding the message bits to match a given code. The $S$ shortened bits are not transmitted, effectively increasing $K$ and $N$, which results in a decreased $R_{\mathrm{c}}$. For LDPC codes shortening can be implemented by disregarding columns of $\mathbf{H}$ as displayed in the figure below.

Repetition code

By applying an additional repetition code $N$ is adjusted upwards, which results in a decreased $R_{\mathrm{c}}$. The repetition coded bits are given with $\hat{c}_i=c_{i \mod \hat{N}}$, for $i \in\{1,...,N\}$, the LDPC pre-coded word $\mathbf{c}$ and $\hat{N}=66Z-S-P$ or $\hat{N}=50Z-S-P$ depending on the base graph.

Taking the rate matching into account, the achievable code rates for fully using the extension part $\mathbf{E}$ are $R_{\mathrm{c}}=\frac{1}{3}$ for BG1 and $R_{\mathrm{c}}=\frac{1}{5}$ for BG2. Lower rates are only achieved via shortening and/or use of the repetition code.