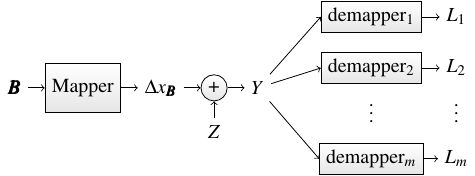
At the receiver, we use a bitwise demapper to calculate soft information for each bit-level and we pass these soft informations to a binary decoder. This combination of a bitwise demapper with a binary decoder is called bit-metric decoding.

• Binary label of $X=S\cdot A$ is $b(S)\mathbf{b}(A)=:B_1B_2\dotsb B_m=:\boldsymbol{B}$.
• We use Gray labeling.
• Denote signal point with label $\boldsymbol{B}$ by $x_{\boldsymbol{B}}$.
• The demapper calculates bitwise soft-information $$ L_j=\log\frac{P_{B_j}(0)}{P_{B_j}(1)}+\log\frac{p_{Y|B_j}(Y|0)}{p_{Y|B_j}(Y|1)},\quad j=1,\dotsc,m. $$
• Achievable rate for bit-metric decoding: $$ \mathsf{R}_\text{BMD}(P_X,\text{SNR})=\Bigl[H(\boldsymbol{B})-\sum_{i=1}^m H(B_i|Y)\Bigr]^+. $$
• No iterative demapping!

G. Böcherer, Achievable Rates for Shaped Bit-Metric Decoding, submitted to IEEE Trans. Inf. Theory, revised.