Error-correcting codes are used to improve the reliability of transmission over noisy channels. The main idea is to add some well-structured redundancy, which helps the receiver to recover the transmitted data, despite of the noise introduced by the channel.
In this webdemo, we are interested in the following linear block codes.

Code 1 (Repetition code):

The repetition code is the simplest error-correcting code, in which every symbol is repeated $n$ times, where $n$ is the codeword length.
Example for $n=2$:

• Bit sequence to be encoded: 10010
• Encoded sequence: 11 00 00 11 00

The repetition code has a minimum hamming distance $d_{min}=n$.

Odd length repetition codes (i.e., $n$ is odd) are perfect codes.

Code 2:

Code rate $r=\frac{k}{n}=\frac{1}{2}$.

The valid codewords are:

\begin{align*} M_{code2}= \left(\begin{array}{cc|cc} 0 &0&0&0\\ 0&1&1&0\\ 1&0&1&1\\ 1&1&0&1 \end{array} \right) \end{align*}

Thus the encoding rule can be expressed as $\mathbf{c}=(\mathbf{u},u_1 \oplus u_2,u_1$).

Code 3:

Code rate $r=\frac{k}{n}=\frac{1}{2}$.

The valid codewords are:

\begin{align*} M_{code3}= \left(\begin{array}{ccc|ccc} 0&0&0&0&0&0\\ 0&0&1&0&1&1\\ 0&1&0&1&0&1\\ 0&1&1&1&1&0\\ 1&0&0&1&1&0\\ 1&0&1&1&0&1\\ 1&1&0&0&1&1\\ 1&1&1&0&0&0 \end{array} \right) \end{align*}

Thus the encoding rule can be expressed as $\mathbf{c}=(\mathbf{u},u_1 \oplus u_2,u_1 \oplus u_3,u_2 \oplus u_3$).

Code 4 ((8,4) extended Hamming code):
We first describe the (7,4) Hamming code in the following

• The original message is composed of 4 bits
• 3 redundancy bits are added to detect and correct errors
• Thus the code has a length of 7
• The original message $\mathbf{d}= \left[d_1,d_2,d_3,d_4 \right]$ is mapped to a codeword $\mathbf{c}=\left[P_1,P_2,d_1,P_3,d_2,d_3,d_4 \right]$, where the parity bits are calculated as follows

\begin{align*} P_1 &= {d_1} \oplus{d_2} \oplus{d_4}\\ P_2 &= {d_1} \oplus{d_3} \oplus{d_4}\\ P_3 &= {d_2} \oplus{d_3} \oplus{d_4} \end{align*}
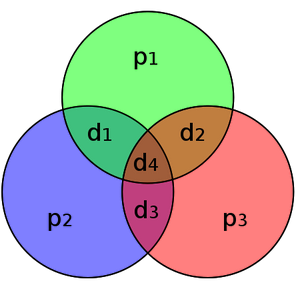
An extra parity bit $P_4$ is added to the (7,4) Hamming code and thus called (8,4) extended Hamming code. The parity bit $P_4$ is calculated as follows
\begin{align*} P_4= {P_1}\oplus{P_2}\oplus{d_1}\oplus{P_3}\oplus{d_2}\oplus{d_3}\oplus{d_4} \end{align*}

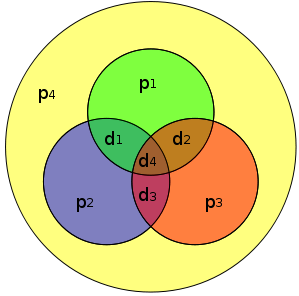
The main parameters of the (8,4) extended Hamming code can be summarized as follows

• Code rate $r=\frac{k}{n}=\frac{1}{2}$
• Minimum Hamming distance $d_{min}=4$
• Thus can detect up to $3$ bits errors
• Can correct $1$ bit error

Hamming codes are "perfect codes".