Binary Symmetric Channel (BSC):

The BSC has two inputs {0,1} and two outputs {0,1}.

The bit is transmitted correctly with a probability $1-\delta$.

$\delta$ is the probability that the bit was "flipped", namely transition probability.

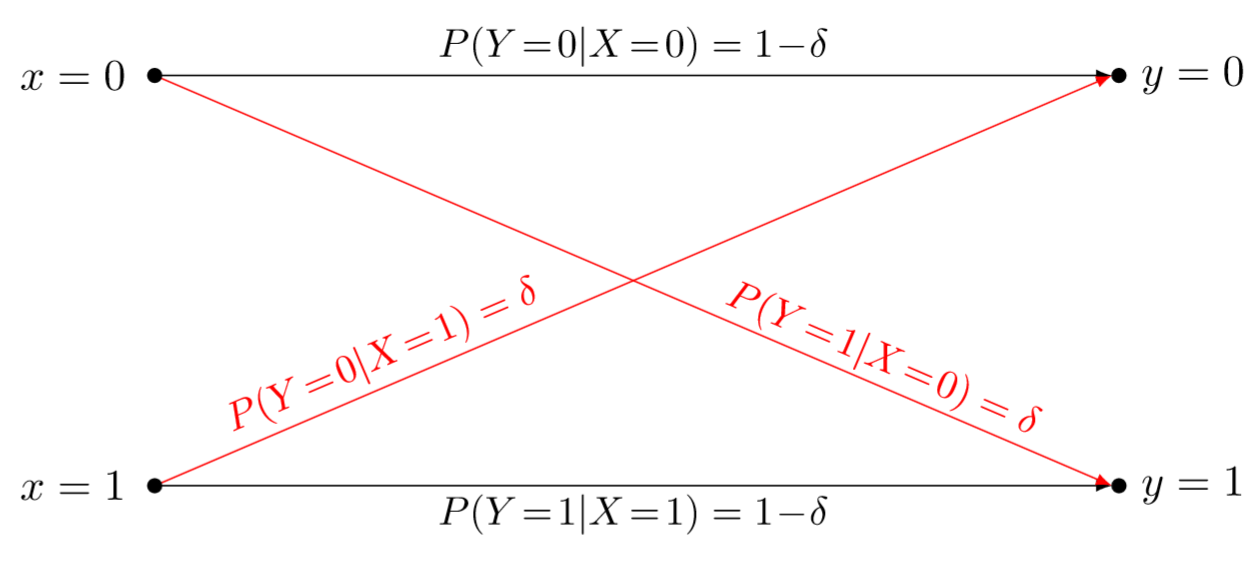
The channel transition matrix of a BSC is:

\begin{align*} T= \left(\begin{array}{cc} 1-δ&δ\\ δ&1-δ \end{array} \right) \end{align*}

The capacity $C$ of a BSC is:

\begin{equation} C = 1-h(\delta) \end{equation}

where $h(\delta)$ is the binary entropy function defined as:

\begin{equation} h(\delta)=-\delta \cdot \log_2(\delta)-(1-\delta) \cdot \log_2(1-\delta) \end{equation}

The BSC is used for modeling hard-decision channels.

Binary Erasure Channel (BEC):

The BEC has two inputs {0,1} and three outputs {0,?,1}.
The third channel output symbol "?" is introduced denoting an erasure i.e., no information is available about the transmitted symbol.

The channel transition matrix of a BEC is:

\begin{align*} T= \left(\begin{array}{cc} 1-ε& 0\\ ε& ε\\ 0 &1-ε \end{array} \right) \end{align*}

where $\epsilon$ is the erasure probability

The capacity $C$ of a BEC is:

\begin{equation} C = 1- ε \end{equation}

The BEC is used for modeling channels with erasures or channels with high signal-to-noise ratio and three-level quantization.

AWGN Channel:

The Additive White Gaussian Noise (AWGN) channel is the most popular channel model and it is mathematically described as follows:

\begin{equation} y_k = x_k + n_k , \hspace{0.5cm} y_k \in \mathbb{R} \end{equation}

• $x_k$ is the transmitted symbol
• $y_k$ is the received symbol
• $n_k$ is the noise sample, which is drawn from a gaussian distributed random variable with zero mean ($μ=0$) and variance $\sigma_n^2$

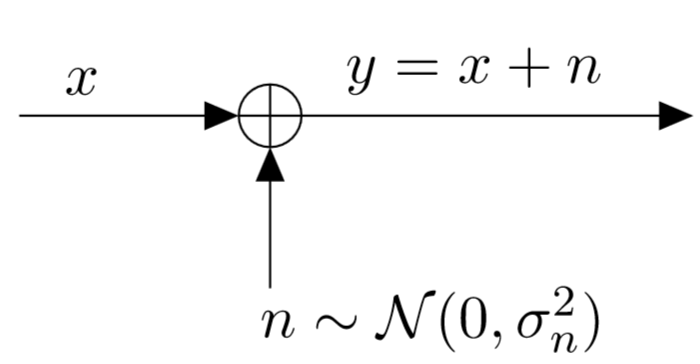
The channel is characterised by the parameter "signal-to-noise-ratio", which is the signal power versus the noise power:

\begin{equation} SNR=\frac{E_s}{N_0}=\frac{E_s}{2 \sigma_n^2}=\frac{1}{2 \sigma_n^2} \end{equation}

$E_s$ denotes the power of the input signal. We usually consider the energy of the transmitted symbol $E_s$ as $1$: \begin{equation} E_s=\mathbb{E} \left\{|x|^{2} \right\}=1 \end{equation}

The AWGN channel model can be applied in several applications such as:

• Satellite communications
• Deep Space communications
• Wireless communications

BI-AWGN Channel:

The Binary Input-AWGN (BI-AWGN) channel is a more relevant channel model. In this model, the input $x$ takes two values $x$ $\in$ {0,1}. This channel can model for instance the common BPSK modulated channel. When transmitting a binary codeword over the BI-AWGN channel, the codeword bits $c_i\in$ {0,1} will be mapped to the symbols $x_i\in$ {1,-1}.

The system model of the BI-AWGN channel is shown in the following figure:

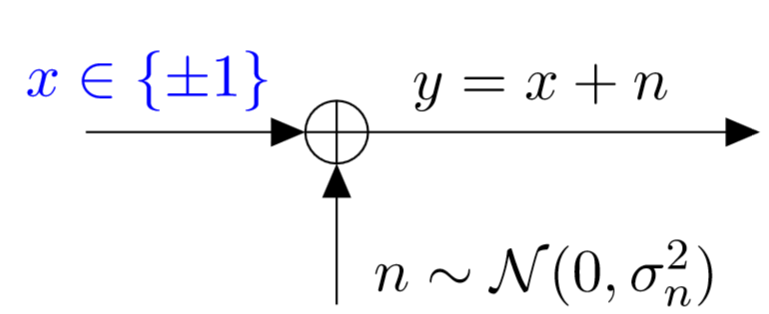
Hard-Decision BI-AWGN Channel:

We obtain this channel by placing a hard decision circuit at the output of a BI-AWGN channel:

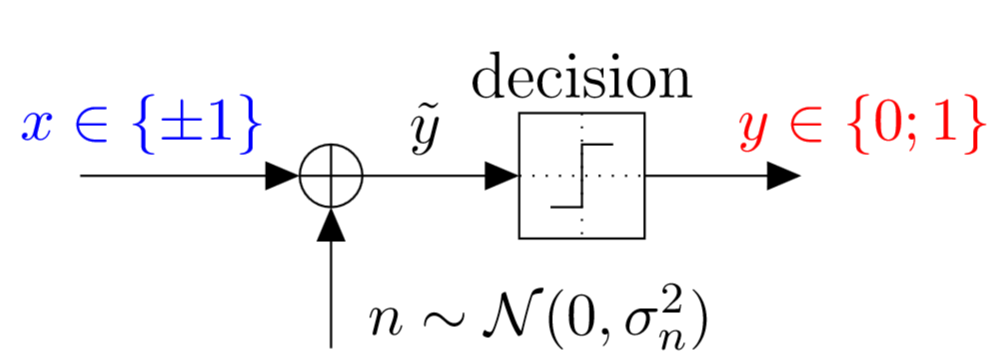
The channel output $y$ is then obtained as follows:
\begin{equation} y= \begin{cases} 0& \text{if} \ \tilde{y}\geq{0} \\ 1& \text{else} \end{cases} \end{equation}

The hard-decision BI-AWGN channel is a BSC with error transition probability $\delta$:

\begin{equation} \delta=Q\left(\frac{1}{\sigma_n}\right)=Q\left(\sqrt{2\frac{E_s}{N_0}}\right)=Q\left(\sqrt{2R\frac{E_b}{N_0}}\right)=\frac{1}{2} \text{erfc} \left(\sqrt{\frac{E_s}{N_0}}\right) \end{equation}

The SNR can be expressed in terms of $\frac{E_b}{N_0}$ or $\frac{E_s}{N_0}$, in which $E_b$ denotes the energy per information bit and $E_s$ denotes the energy per symbol.

To compare different coding schemes with different code rates, $\frac{E_b}{N_0}$ is used instead of $\frac{E_s}{N_0}$ i.e., $\frac{E_b}{N_0}$ takes into consideration the code rate.

The relationship between $\frac{E_b}{N_0}$ and $\frac{E_s}{N_0}$ is:

\begin{equation} \frac{E_s}{N_0}={r}\cdot{\frac{E_b}{N_0}}={\frac{k}{n}} \cdot {\frac{E_b}{N_0}} \end{equation}

\begin{equation} \frac{E_s}{N_0}\bigg|_{dB}=\frac{E_b}{N_0}\bigg|_{dB}+10 \cdot \log_{10} (r)=\frac{E_b}{N_0} \bigg|_{dB}+10 \cdot \log_{10} \left(\frac{k}{n}\right) \end{equation}