With hard decision at the receiver, information about the reliability of the decision is lost. Soft decision considers how reliable decisions are. An indicator for this could be the distance of the received value $y$ to the threshold. The performance of equalization and decoding can be tremendously increased by soft decision.

A measure of the reliability is the so called log-likelihood ratio (LLR) or L-value. The L-value extends the binary value to an analog value ("soft bit", "soft value"). The L-value is defined for a signal with BPSK modulation as

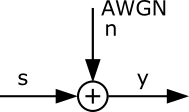
\[ L(s|y) = \ln\frac{P[s=+1|y]}{P[s=-1|y]}.\] $s$ is the transmitted symbol and $y$ is the received symbol which is affected by AWGN according to the figure.

$$ $$

$$ $$

$$ $$

For simplicity of presentation, the amplitude values of the constellation points are not normalized to $ E[|s|^2]=1 $ in this demo.

Note that, throughout this demo, for the (complex) additive white Gaussian noise $n=n_\mathrm{re}+j n_\mathrm{im}$, by convention, we set $E[|n_\mathrm{re}|^2])=E[|n_\mathrm{im}|^2]=\sigma^2$ such that $E[|n|^2]=2 \sigma^2$, and $\mathrm{SNR}=1/(2 \sigma^2)$.