The aim of constructing a source code using the Huffman algorithm is to minimize the average codeword length. In fact, codes constructed using this algorithm can be shown to have the minimum achievable average codeword lengths wich are as close as possible to the entropy of the given source.

This webdemo shows how a code is created based on a given source with specified probabilities of ocurrence of contained symbols. For this, the following algorithm is implemented:

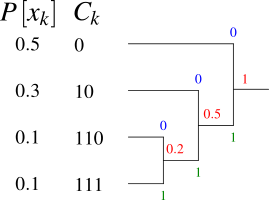
1. Order the symbols $x_k$ by non-accending probabilities of ocurrence $P_k$.
2. Combine two least-probable symbols into a new one, assign the sum of the two original probabilities to be the probability of the new symbol.
3. In the set of symbols, replace the two symbols found in step 2 as least probable by the new symbol.
4. Repeat steps 1 to 3 until one symbol with the probability 1 remains.
   • The graph present now is a binary tree with the original symbols being the leafs, the combination points from repeated step 2 being the branch points and the single last symbol the trunk or the root.
5. Starting from the trunk, going towards the leafs, assign "0" or "1" to each branch.
6. When reading from the trunk towards the leafs, the string of zeros and ones on the path build the codeword of the corresponding leaf.

The resulting code has also the property that in the stream of encoded symbols, the ones and zeroes are almost equally probable, although not quite exactly. Obviously, there is a degree of freedom regarding the assignment of "0" and "1" to the branches. If at every join the more probable branch is given the value "0", then the value "0" is also slightly more probable than "1" in the bit stream. This can be influenced in the webdemo.

Another degree of freedom is the choice among symbols with possibly equal probabilities, which one to use in step 2 for combining into a new symbol. The choice influences the shape of the tree and the distribution of the codeword lengths (although the same minimum average codeword length is achieved regardless of this choice). In the webdemo, the design rule is being followed that after re-sorting the symbols when repeating the step 1, the newly created symbol is moved upwards even if it has the same probability as one or several leaf symbols originally present in the source. The effect is that, among equally probable symbols, leafs are preferred in the choice which symbols to combine every time step 2 is executed. This, in turn, results in a code that shows a minimum variance of codeword lengths.