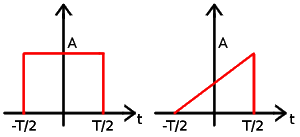
With mathematical manipulations, the expression from the previous slide can be transformed into time-domain. The inverse Fourier-transform yields $$ u(x,t) = \frac{1-r_1}{2} \sum_{n=0}^{\infty}(r_1r_2)^ne^{-\alpha(2\ell n+x)}u_0\left(t-\frac{2\ell n+x}{v_{ph}}\right) + \frac{1-r_1}{2}r_2 \sum_{n=0}^{\infty}(r_1r_2)^ne^{-\alpha(2\ell (n+1)-x)}u_0\left(t-\frac{2\ell (n+1)-x}{v_{ph}}\right) $$ In the following demonstration, either a rectangular or a triangular impulse with length $T$ can be sent over a line. Reflection coefficients $r_1$, $r_2$ as well as $v_{ph}$, $\ell$, and $\alpha$ can be set by the user. The option "dynamic scaling" adapts the y-axis scale according to the impulse height.
The demo shows $u(x,t_0)$ over $x$ for various $t_0$.

Attenuation $\alpha$ is given in $\frac{\text{Np}}{\text{m}}$ and can be converted in $\frac{\text{dB}}{\text{m}}$ by $$ \left. \alpha \right|_{dB} \approx 8.686 \cdot \left. \alpha \right|_{Np} $$