A system with multiple transmit and multiple receive antennas (also known as MIMO system) is capable of increasing data rate applying spatial multiplexing. In spatial multiplexing, the high-rate bitstream is split into multiple low-rate bitstreams which are simultaneously transmitted by different antennas using the same frequency band. The transmitted signals arrive receiver through different propagation paths, which induces interference between substreams. In order to separate the sub-streams from each other at receiver, a detector (equalizer) is needed. Stacking the received signals at each antenna into a vector, the MIMO signal can be expressed by a matrix-vector equation as $$ \mathbf{r}=\mathbf{H}\cdot \mathbf{s}+\mathbf{n} \mathrm{,} $$ where $\mathbf{r} \in \mathbb{C}^{\mathrm{N} \mathrm{x} 1}$ is the equivalent complex baseband received signal before detector and $\mathbf{s} \in \mathbb{C}^{\mathrm{M} \mathrm{x} 1}$ is the transmitted signal. Furthermore, $\mathbf{n}$ denotes the additive white Gaussian noise with zero-mean and covariance matrix $\sigma_{n}^2\mathbf{I}$, i.e., spatially uncorrelated noise. The MIMO channel is assumed to exhibit flat fading property, which is modeled by the matrix $\mathbf{H}$ with independently identical distributed elements. The individual element of $\mathbf{H}$ follows complex Gaussian distribution with zero mean and unit variance.


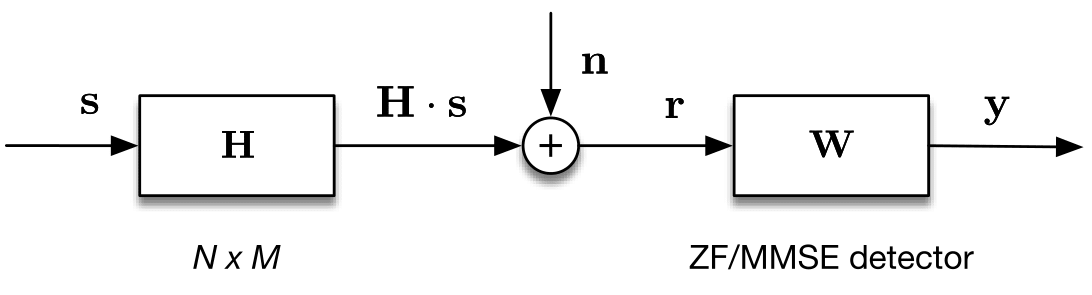
With a linear receiver, modeled by receive matrix $\mathbf{W}$, the estimated signals can be expressed as $$ \mathbf{y}=\mathbf{W} \cdot \mathbf{r}=\mathbf{W}\mathbf{H}\mathbf{s}+\mathbf{W}\mathbf{n} $$ Zero-Forcing detecor suppresses the Inter-Stream Interference (ISI) to zero, so that it must be fulfilled $$ \mathbf{W}\mathbf{H} \overset{!}{=} \mathbf{I} \mathrm{,} $$ The solution for an overdetermined MIMO system, i.e., $N_{\mathrm{rx}}>N_{\mathrm{tx}}$, is given by the Moore-Penrose Inverse $$ \mathbf{W}=(\mathbf{H}^H\mathbf{H})^{-1}\mathbf{H}^H $$ One main drawback of ZF detecor is it enhances noise power, in particular for ill-conditioned channels.

Minimum-Mean-Square-Error detector considers also the noise statistics in the optimization procedure and minimize the overall estimation error. The optimization problem can be formulated as $$ \underset{\forall \mathbf{w}}{\mathrm{min}} \quad J = E[\Vert \mathbf{y}-\mathbf{s} \Vert^2] $$ The solution to the optimization problem above is given by $$ \mathbf{W}=(\mathbf{H}^H\mathbf{H}+\sigma_{n}^2\mathbf{I}_M)^{-1}\cdot\mathbf{H}^H $$