Non-linear MIMO detection methods
In this slide, two conventional non-linear detectors, i.e., Maximum Likelihood (ML) and Successive Interference Cancellation (SIC) detector are discussed.
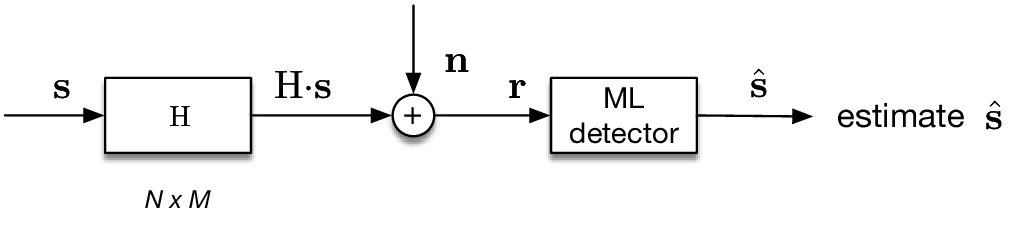
Maximum Likelihood detector performs a brute-force search over all possible combination of transmitted data symbols. This detector computes the likelihood probability (or other equivalent metrics, e.g., Log-Likelihood-Ratio) for all $\mathrm{B^M}$ possible transmitted symbol candidates, which is determined by the number of constellation point $B$ and the number of transmit antenna $M$. Then, the most probable candiate is selected as final symbol estimate. The likelihood-based decision rule is given by
$$ \hat{\mathbf{s}} \triangleq \mathrm{arg} \ \underset{\mathbf{s}\in B^M}{\mathrm{max}}\quad P(\overbrace{\mathbf{r}}^{\mathrm{received}} \mid \overbrace{\mathbf{H} \cdot \mathbf{s}}^{\text{transmitted, } \mathbf{s} \text{ through known channel}}) $$
The ML detector can achieve the best performance. However, the complexity increases exponentially if higher order QAM or larger number of transmit antenna is applied. Thus, this algorithm is prohibited for large constellation size and MIMO size.

Successive Interference Cancellation detector is a recursive detection algorithm using decision-feedback to increase diversity. Instead of simultaneously detecting all transmitted data symbols, the data symbols are successively detected and the already detected symbols are cancelled out from the MIMO system. By doing this, additional diversity can be achieved for next step, provided that all previous decisions are correct. To minimize the error propagation effect, the more reliable data vector components should be detected first. Usually, this method is combined with linear receiver such as ZF and MMSE.

Maximum Likelihood detector performs a brute-force search over all possible combination of transmitted data symbols. This detector computes the likelihood probability (or other equivalent metrics, e.g., Log-Likelihood-Ratio) for all $\mathrm{B^M}$ possible transmitted symbol candidates, which is determined by the number of constellation point $B$ and the number of transmit antenna $M$. Then, the most probable candiate is selected as final symbol estimate. The likelihood-based decision rule is given by
$$ \hat{\mathbf{s}} \triangleq \mathrm{arg} \ \underset{\mathbf{s}\in B^M}{\mathrm{max}}\quad P(\overbrace{\mathbf{r}}^{\mathrm{received}} \mid \overbrace{\mathbf{H} \cdot \mathbf{s}}^{\text{transmitted, } \mathbf{s} \text{ through known channel}}) $$
The ML detector can achieve the best performance. However, the complexity increases exponentially if higher order QAM or larger number of transmit antenna is applied. Thus, this algorithm is prohibited for large constellation size and MIMO size.

Successive Interference Cancellation detector is a recursive detection algorithm using decision-feedback to increase diversity. Instead of simultaneously detecting all transmitted data symbols, the data symbols are successively detected and the already detected symbols are cancelled out from the MIMO system. By doing this, additional diversity can be achieved for next step, provided that all previous decisions are correct. To minimize the error propagation effect, the more reliable data vector components should be detected first. Usually, this method is combined with linear receiver such as ZF and MMSE.
