This webdemo also covers linear binary block codes. Each block code has a specific generator matrix of dimension $ k \times n $, as shown exemplarily in the figure on the right. In a generator matrix, each row contains one generator. Messages $\textbf{m}$ are encoded with a generator matrix $ \textbf{G} $ into codewords $\textbf{c}$:
$$ \textbf{c} = \textbf{m} \cdot \textbf{G} $$
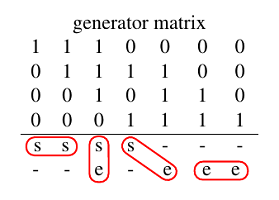
Trellis diagrams of linear binary block codes can be created using a trellis oriented generator matrix [1]. In a trellis oriented generator matrix the first and last entry of each row are the only non-zero entries in their column. The shown generator matrix on the right is in trellis oriented form. A trellis created from a trellis oriented generator matrix is a minimal trellis in which a maximum of two edges emerge from a state or enter a state. Block code trellises have a worst case maximum state amount of $2^k$ states.

Trellis diagrams in this webdemo are compressed with a heuristic compression rule [2]. It defines how to merge trellis segments in order to recieve a small amout of states per time instance while still having a minimal trellis. According to this rule, several codeword bits are combined into one segment based on the trellis oriented generator matrix. For each segment in the compressed trellis diagram, all bits between a start bit of any generator and an endbit of any generator are combined. Start bits and end bits are marked with "$\mathrm{s}$" and "$\mathrm{e}$" underneath the generator matrix on the right. In sections where only start bits or only end bits occur in sequence, they are combined all together. An example of the execution of this rule is shown with red edging underneath the trellis oriented generator matrix on the right.