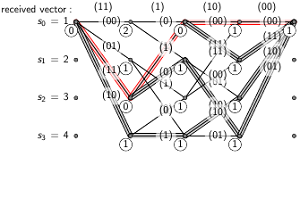
Viterbi algorithm
$$ B_{I,p} = \sum_{i=0}^{I}b_{i,p}. $$
When two edges enter a state, the Viterbi algorithm selects the one with smaller path metric as the survivor path, while the path with larger path metric dies.
The hard decision Viterbi algorithm calculates branch metrics based on the Hamming distance $ d_{\mathrm{H}} $ between codeword bits $c_{i,p}$ and the received symbols from a binary symmetric channel $r_{i,p}$: $$ b_{\mathrm{H},i,p} = d_{\mathrm{H}}(c_{i,p},r_{i,p}) = |c_{i,p}-r_{i,p}|. $$
The soft decision Viterbi algorithm calculates branch metrics based on the squared Euclidean distance $ \Delta[\cdot] $ between codeword bits $c_{i,p}$ and the received symbols from an additive white Gaussian noise channel $r_{i,p}$:
$$ b_{\mathrm{S},i,p} = \Delta [c_{i,p},r_{i,p}]= (c_{i,p}-r_{i,p})^2. $$
