Decoding Performance of SC-LDPC Codes
In principle, each block code can be decoded with a maximum a posteriori (MAP) decoder. However, the decoding complexity becomes $\mathcal{O}(n^3)$ for the BEC, which is infeasible for large $n$.
In the case of LDPC codes a very easy decoding algorithm exists - the so-called belief propagation (BP) algorithm [3]. This algorithm is based on the Tanner graph of the LDPC code. For further details see webdemo Peeling Decoder and Exit Charts.
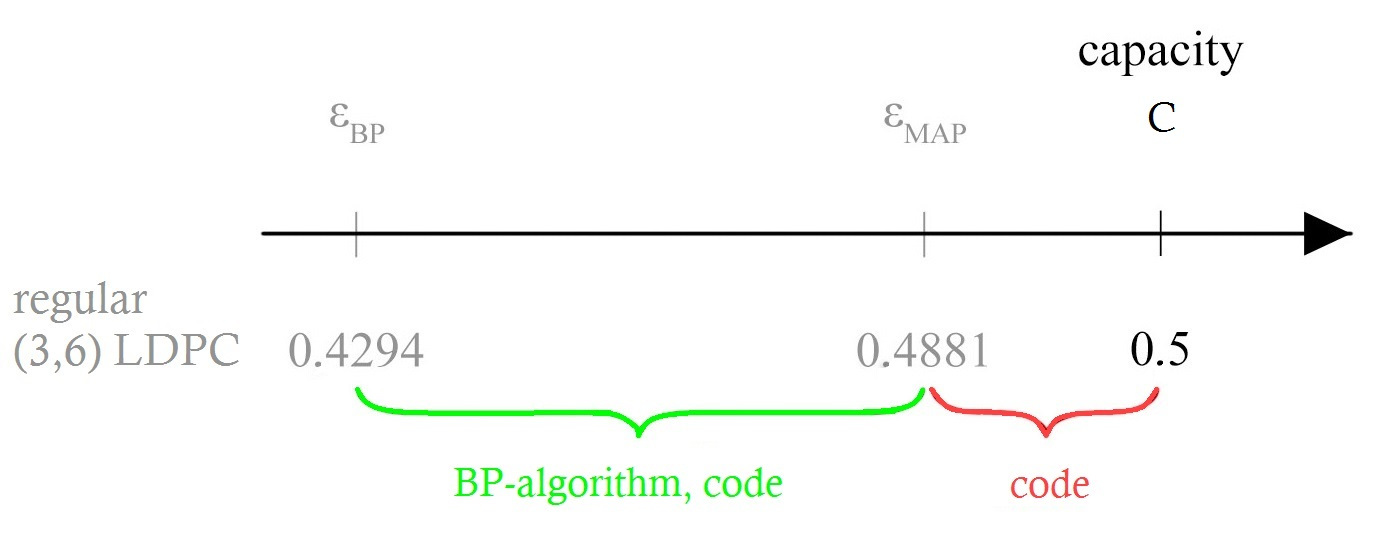
There is a gap between the BP and the MAP performance of a code. This gap can be closed by changing the decoder AFTER receiving the message. The gap between the MAP performance and the capacity cannot be closed by changing the decoding algorithm. It depends on the specific code, therefore this gap can only be closed by changing the code structure.
In the case of LDPC codes a very easy decoding algorithm exists - the so-called belief propagation (BP) algorithm [3]. This algorithm is based on the Tanner graph of the LDPC code. For further details see webdemo Peeling Decoder and Exit Charts.
There is a gap between the BP and the MAP performance of a code. This gap can be closed by changing the decoder AFTER receiving the message. The gap between the MAP performance and the capacity cannot be closed by changing the decoding algorithm. It depends on the specific code, therefore this gap can only be closed by changing the code structure.

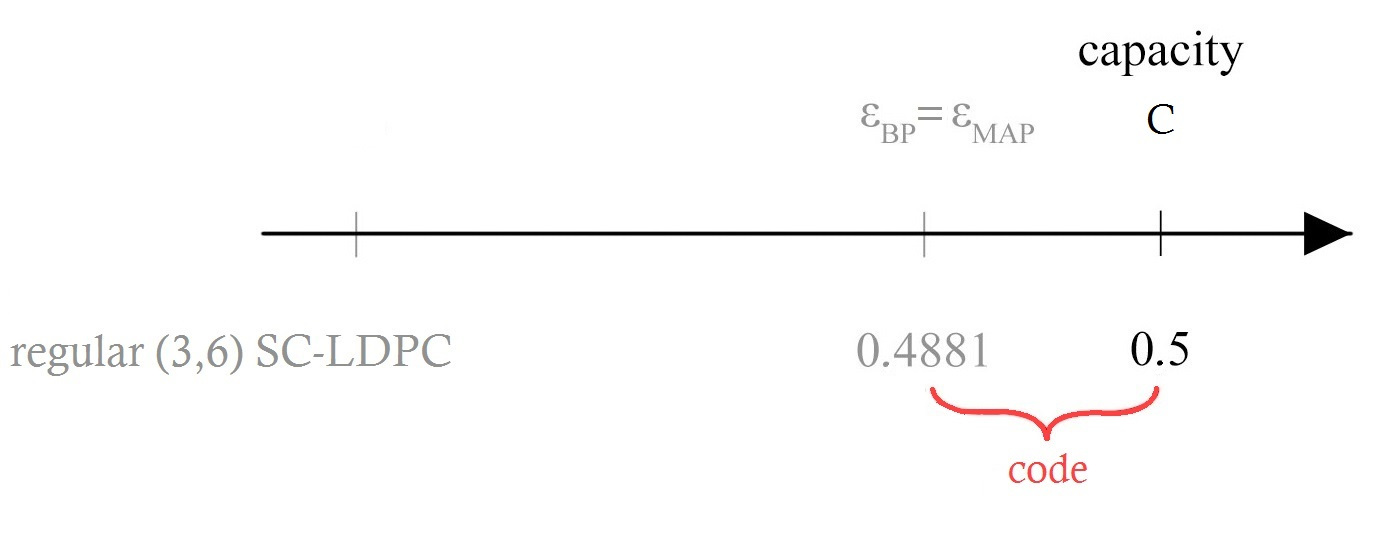
In the case of SC-LDPC codes, it can be shown that they reach the MAP performance of the underlying block LDPC code under BP decoding [4].

The BP threshold $\varepsilon_{BP}$ and MAP threshold $\varepsilon_{MAP}$ of a regular $(d_v,d_c)$ block LDPC codes can be seen in the following table:
| $\left(d_{v},d_{c}\right)$ | $\varepsilon_{\mathrm{BP}}$ | $\varepsilon_{\mathrm{MAP}}$ |
| $\left(2,4\right)$ | $0.3287$ | $-$ |
| $\left(3,6\right)$ | $0.4294$ | $0.488$ |
| $\left(4,8\right)$ | $0.3835$ | $0.498$ |
| $\left(5,10\right)$ | $0.3416$ | $0.499$ |
| $\left(6,12\right)$ | $0.3075$ | $0.4999$ |
