Density Evolution for Block LDPC Codes

The expected behavior of the BP algorithm can be simulated with the density evolution (DE) [5]. The DE is a very powerful tool to investigate the performance of LDPC codes under BP-decoding, as no demanding BER simulation is necessary.

Assuming the BEC$\left(\varepsilon\right)$ and a regular block LDPC $\left(d_{v},d_{c}\right)$ ensemble without circles under BP decoding.

We define ${x}$ as the averaged erasure probability of a message (respectively the node) from an arbitrary variable node and ${y}$ as the averaged erasure probability of a message from an arbitrary check node.

The decoding progress consist of two parts

• check node upgrade: equals a single parity check, therefore all ${d_{c}-1}$ incoming messages ${x}$ must be known. The probability that this equation cannot be solved is $y=1-\left(1-x\right)^{d_{c}-1}$

• variable node upgrade: equals a repetition code, therefore at least one out of the ${d_{v}-1}$ incoming message ${y}$ or the channel output must be known to reconstruct the variable node $x=\varepsilon\left(y\right)^{d_{v}-1}$

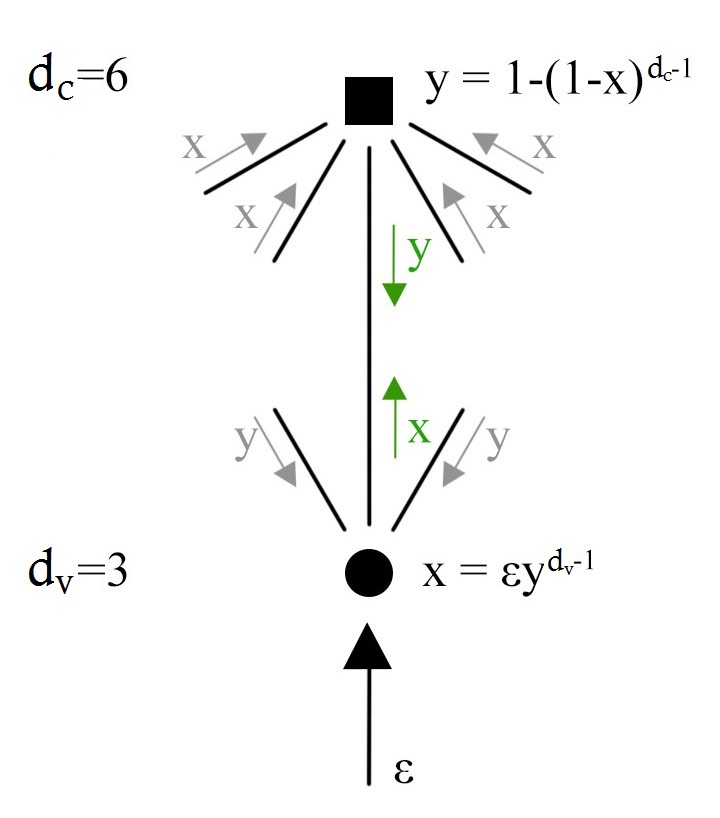
To put it all together, the averaged erasure probability ${x}$ of an arbitrary bit after ${l}$ iterations is $$x^{\left[l\right]}=\varepsilon\underset{y}{\underbrace{\left(1-\left(1-x^{\left[l-1\right]}\right)^{d_{c}-1}\right)}}^{d_{v}-1}$$

with initialization $$ x^{\left[0\right]}=1. $$

The calculation above is called density evolution and indicates an expected BER after ${l}$ decoding iterations for infinite code length. Furthermore, the density evolution gives a threshold $\varepsilon_{BP}$ for which the BP decoder converges to an error free code word after an infinite number of iterations

$$ \varepsilon_{BP}=sup\left\{ \varepsilon\,\in\left[0,1\right]:\,\,x^{\left[l\right]}\overset{l\rightarrow\infty}{\rightarrow}0\,\,\forall x\right\} . $$

Stopping Criteria

For numerical implementations, the density evolution needs to be stopped after a certain number of iterations. There are mainly two ways of stopping the density evolution

1. Stop after a fixed number of iterations ${N_{it}}$

2. Define a threshold ${\mu}$ and stop if ${\mu>}$ $\underset{i}{\sum}\left(x_{i}^{\left[l\right]}-x_{i}^{\left[l-1\right]}\right)$

Density Evolution for SC-LDPC Codes with Random Structure

Analog to the density evolution of block LDPC codes, the density evolution of a SC-LDPC code can be derived by calculating the erasure probabilities of variable and check nodes with respect to their spatial position ${i}$ (variable node position), ${j}$ (check node position) and the coupling length ${W}$ [6].

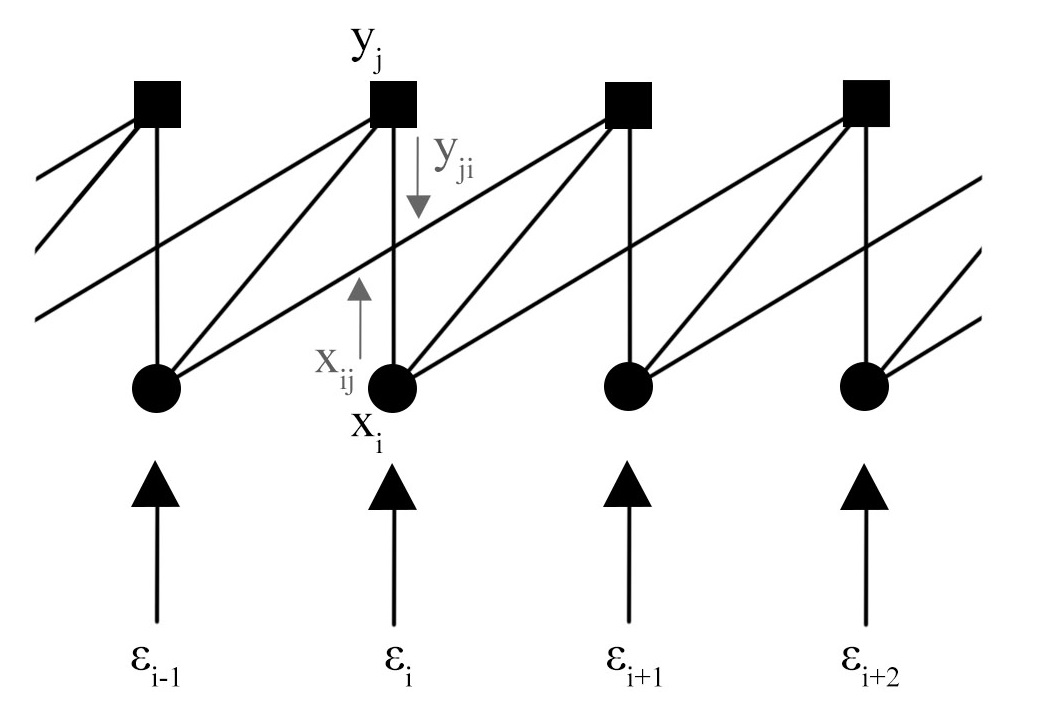
Each check node can be connected to random variable nodes within a range of ${W}$ blocks.

We define

• ${x_{i}}$ as the averaged erasure probability of a random variable node in block ${i}$

• ${y_{j}}$ as the averaged erasure probability of a random check node in block ${j}$

The source of a message is unknown, because it can be sent from any connected check node within $W$. We assume ${d_{v}}-1$ (respectively $d_{c}-1$ ) incoming messages with the averaged erasure probability of all connected ${W}$ blocks of check nodes (respectively variable nodes).

This message is broadcasted to all connected check nodes (respectively variable nodes).

The messages from VND to CND are

$$ x_{i}=\varepsilon_{i}\cdot\left(\frac{1}{W}\cdot\sum\limits_{k=0}^{W-1}y_{i+k}\right)^{d_{v}-1}. $$

With analog considerations for the check nodes it holds

$$ y_{j}=\left(1-\frac{1}{W}\cdot\sum\limits_{k=0}^{W-1}\left(1-x_{j-k}\right)\right)^{d_{c}-1}. $$

The initialization must be extended to $$ x_{i}^{\left[0\right]}=1\,\,\forall i. $$

Note that $(\mathit{i+k)}$ and $(\mathit{j-k)}$ is a circular shift, i.e. $(\mathit{j-k})$ is replaced by $(\mathit{j-k+L)}$ if $(\mathit{\mathit{j-k)<0}}$ and $(\mathit{\mathit{i+k)}}$ is replaced by $(\mathit{\mathit{i+k}}-L)$ if $(\mathit{\mathit{i+k})}\geq L$. The equations are valid for tail-biting SC-LDPC codes. For a terminated code the length must be extended to $\mathit{L'=L+W}-1$ and the last $\mathit{W-1}$ variable nodes $x_{i}$ must be initialized with zero, since the blocks are frozen and therefore perfectly known.

These update equations are more complex than the ones for block LDPC, but can be solved numerically.

Finally, the density evolution of SC-LDPC codes gives the expected local BER for each spatially position. Therefore, it is a helpful tool to visualize and investigate the BP decoding progress.