An arbitrary block $(d_v, d_c)$ LDPC code can be extended to an SC-LDPC code within 4 steps:

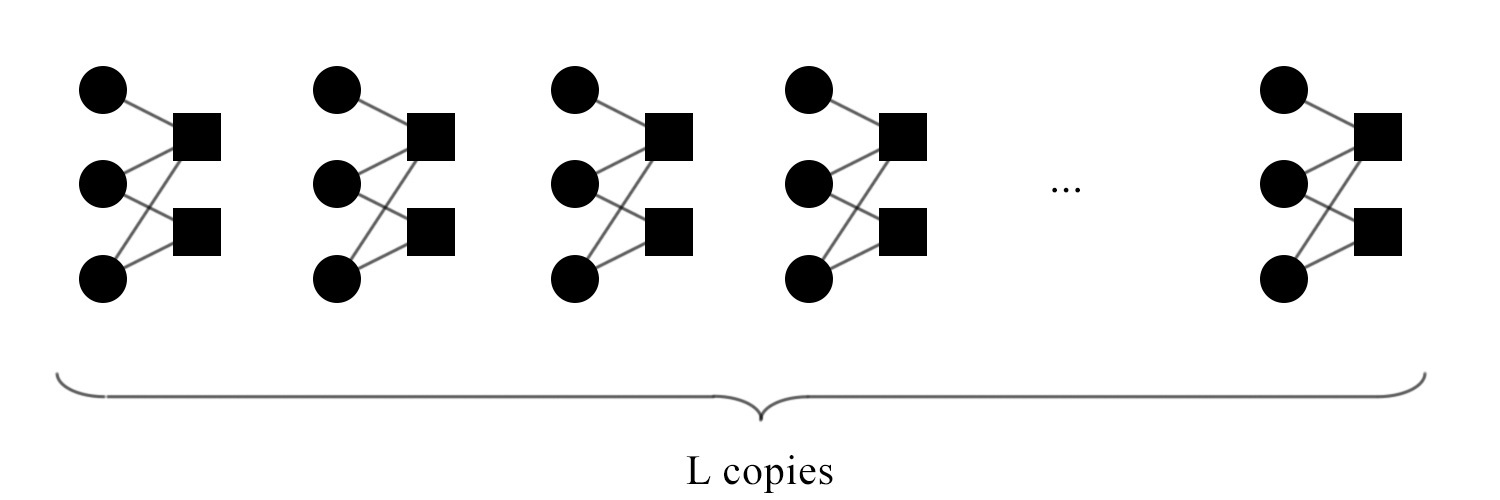
1. The underlying block LDPC code is represented as a Tanner graph

2. The underlying block LDPC code is copied $L$ times ($L$ is called replication factor, e.g. $L=50$), which is equal to $L$ different, independent code words.

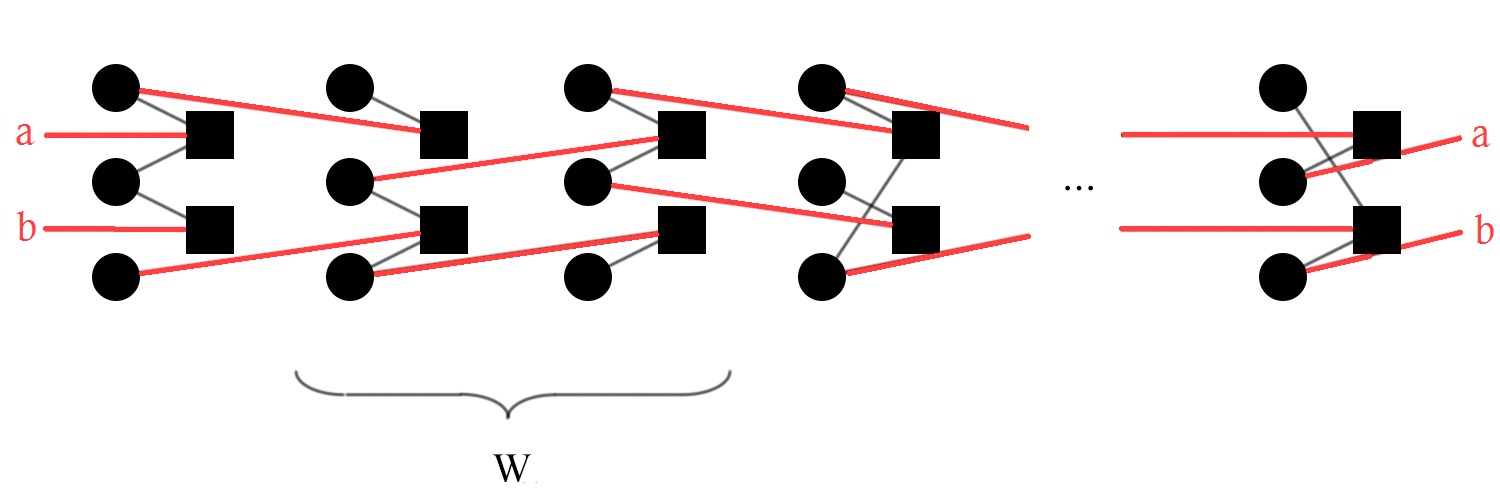
3. The edges of these $L$ underlying block LDPC codes are randomly permuted inside a coupling window $W$ (e.g. $W=3$)

4. The code must be terminated after $L$ replications, several principles exist. Basically the last $W-1$ blocks must be protected by additional parity bits. This sequence does not contain information bits and therefore the code rate decreases. This results in a communication overhead, which can be mitigated by a large replication factor (see the following slide for details).
It is a current topic in research how to avoid or mitigate this rate loss.